题目内容
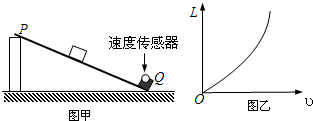
(15分)如图甲所示,质量m1=2.0 kg 的物块A随足够长的水平传送带一起匀速运动,传送带的速度大小v带=3.0 m/s,方向如图所示;在A的右侧L=2.5 m 处将质量m2=3.0 kg的物块B无初速度放上传送带.已知在A、B碰后瞬间B相对传送带的速度大小为1.0 m/s,之后当其中某一物块相对传送带的速度为零时,传送带立即以大小为2.0 m/s2的加速度制动,最后停止运动.传送带的运动情况不受物块A、B的影响,且A、B碰撞的时间极短.设两物块与传送带间的动摩擦因数均为μ=0.10.求:
(1)物块B刚开始滑动时的加速度.
(2)碰撞后两物块的速度.
(3)两物块间的最大距离.
![]()
甲
【解析】(1)物块B刚开始滑动时,加速度为:
a=![]() =μg=1 m/s2,方向向右. (2分)
=μg=1 m/s2,方向向右. (2分)
(2)设经t1时间,A、B两物块相碰,有:
![]() at
at![]() +L=v带t1
+L=v带t1
解得:t1=1 s,t1′=5 s(由上述分析可知,t1′不合题意,舍去)
碰前B的速度v2=at1=1 m/s (2分)
由题意可知:碰后B的速度v2′=2 m/s或v2″=4 m/s
由动量守恒定律得:
m1v带+m2v2=m1v1′+m2v2′
m1v带+m2v2=m1v1″+m2v2″
解得:碰后A的速度v1′=1.5 m/s或v1″=-1.5 m/s
检验:由于![]() m1v
m1v![]() +
+![]() m2v
m2v![]() <
<![]() m1v1′2+
m1v1′2+![]() m2v2″2
m2v2″2
故v1″=-1.5 m/s、v2″=4 m/s这组数据舍去
所以碰后A的速度v1′=1.5 m/s,方向向右;B的速度v2′=2 m/s,方向向右. (3分)
(3)因碰后两物块均做加速度运动,加速度都为a=1 m/s2,所以B的速度先达到与传送带相同速度,设B达到与传送带速度相同的时间为t2.
有:v带=v2′+at2,t2=1 s
此时A的速度v3=v1′+at2=2.5 m/s<v带
故从t2之后A继续加速运动,B和传送带开始减速运动,直到A和传送达到某个共同速度v4后,A所受的摩擦力换向,才开始减速运动.设A继续加速度的时间为t3,则:
v4=v3+at3=v带-a带t3,t3=![]() s
s
A的速度v4=v3+at3=![]() m/s (2分)
m/s (2分)
此时B的速度v5=v带-at3=![]() m/s,之后A、B均做减速运动,因为在整个过程中B的速度始终大于A的速度,所以当A、B都静止时两物块间的距离最大. (1分)
m/s,之后A、B均做减速运动,因为在整个过程中B的速度始终大于A的速度,所以当A、B都静止时两物块间的距离最大. (1分)
B碰后运动的总位移s2=![]() +
+![]() =7 m
=7 m
或s2=![]() t2+
t2+![]() ×
×![]() =7 m (2分)
=7 m (2分)
A碰后运动的总位移s1=![]() +
+![]() ≈6 m (2分)
≈6 m (2分)
两物块间的最大距离sm=s2-s1=1 m. (1分)
[答案] (1)1 m/s2,方向向左
(2)A的速度为1.5 m/s,方向向右;B的速度为2 m/s,方向向右
(3)1 m

乙

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案


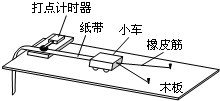 (2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是