题目内容
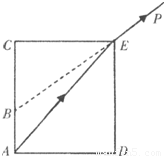
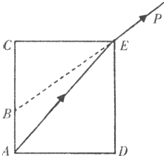如图所示，为了测定水的折射率，某同学将一个高32cm，底面直径24cm的圆筒内注满水，这时从P点恰能看到筒底的A点．把水倒掉后圆筒仍放在原处，这时再从P点观察只能看到B点，B点和C点的距离为18cm．由以上数据计算得水的折射率为多少？若一束光由空气通过圆筒进人水中，则光在水中的传播速度多大（光在真空中速度为3×108m/s）．分析：根据几何关系求出入射角和折射角的正弦，结合折射定律求出水的折射率，通过v=
求出光在水中的传播速度．
| c |
| n |
解答：解：根据几何关系得，sini=
=
=
sinr=
=
=
根据折射定律得，
=
得n=
．
由v=
得，v=2.25×108m/s．
答：水的折射率为
，光在水中的传播速度为2.25×108m/s．
| AD |
| AE |
| 24 | ||
|
| 3 |
| 5 |
sinr=
| AD |
| BE |
| 24 | ||
|
| 4 |
| 5 |
根据折射定律得，
| sini |
| sinr |
| 1 |
| n |
得n=
| 4 |
| 3 |
由v=
| c |
| n |
答：水的折射率为
| 4 |
| 3 |
点评：解决本题的关键掌握光的折射定律，能够熟练运用公式n=
和n=
．
| sinθ1 |
| sinθ2 |
| c |
| v |
练习册系列答案
相关题目
为了测定某额定功率为1000w的电热水器的效率，物理兴趣小组的同学在热水器中加了2kg的水，让热水器正常工作，并绘制出通电加热过程中水温随时间的变化情况图，如图所示，求：
