Question

【题目】匝数为N=100、边长为L=0.5 m、阻值为r=1.5 Ω的正方形导线框与间距为d=0.5 m的竖直导轨相连，正方形线框的上半部分处在水平向外的磁场B1中，导轨的下部存在着水平向里的磁感应强度为B2=1 T的匀强磁场。质量为m=0.2 kg、电阻为R=0.5 Ω的导体棒ab可以沿竖直导轨无摩擦地滑动。当磁场B1发生变化时，导体棒ab刚好能处于静止状态。重力加速度g取10 m/s2，试求：

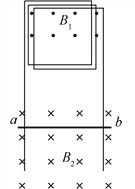
（1）此时通过ab棒的电流I的大小和方向；

（2）此过程中磁场B1的变化率；

（3）开始的5 s内回路中产生的焦耳热Q。

Answer 1

【答案】（1）4 A，方向由a向b（1分） （2）0.64 T/s （3）160 J

【解析】试题分析：导体棒ab静止，所受的安培力与重力平衡，由平衡条件求解通过ab棒的电流I的大小，由左手定则判断电流的方向；根据法拉第电磁感应定律和闭合电路欧姆定律结合求磁场B1的变化率；由焦耳定律求开始的5s内回路中产生的焦耳热Q。

（1）导体棒ab静止，所以有mg=B2IL

解得

由左手定则可知，电流方向由a到b）

（2）根据法拉第电磁感应定律得：

面积为：S=L2/2

根据欧姆定律有：E=I(R+r)

代入数据解得=0.64 T/s

（3）开始的5s内回路中产生的焦耳热为：Q=I2(R+r)t=42×(0.5+1.5)×5 J=160 J