题目内容
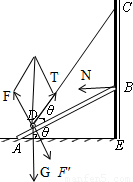
如图所示,一轻绳一端悬于墙面上C点,另一端拴一重为 N的光滑小球,小球搁置于轻质斜面板上,斜面板斜向搁置于光滑竖直墙面上,斜面板长度为AB=L,图中θ角均为30°.则AD= ,墙面受到斜面板的压力为 N.
N的光滑小球,小球搁置于轻质斜面板上,斜面板斜向搁置于光滑竖直墙面上,斜面板长度为AB=L,图中θ角均为30°.则AD= ,墙面受到斜面板的压力为 N.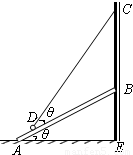
【答案】分析:对小球受力分析可知小球的受力情况,由共点力的平衡条件可得出小球对斜面板的压力;对斜面板由共点力的平衡条件利用三力汇交原理可求得AD长度,再由牛顿第三定律可求得墙面对斜面板的压力.
解答:解:对小球受力分析如图所示,则由几何关系可知: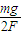 =cos30°
=cos30°
解得:F=100N;
因斜面板处于平衡状态,则A点的支持力、B点的弹力及D点的压力三力应交于一点,由几何关系可知,AD长度应l=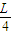 ;
;
对斜面板由力矩平衡的条件可知:
F′l=NLsin30°
解得:N=50N;
故答案为: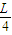 ;50.
;50.
点评:本题用到了三力汇交原理,作用于刚体上的三个相互平衡、但又不互相平行的力,若其中两个力的作用线汇交于一点,则此三力必在同一个平面内,且第三个力的作用线通过前两个力的汇交点.
解答:解:对小球受力分析如图所示,则由几何关系可知:
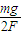 =cos30°
=cos30°解得:F=100N;
因斜面板处于平衡状态,则A点的支持力、B点的弹力及D点的压力三力应交于一点,由几何关系可知,AD长度应l=
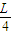 ;
;对斜面板由力矩平衡的条件可知:
F′l=NLsin30°
解得:N=50N;
故答案为:
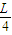 ;50.
;50.
点评:本题用到了三力汇交原理,作用于刚体上的三个相互平衡、但又不互相平行的力,若其中两个力的作用线汇交于一点,则此三力必在同一个平面内,且第三个力的作用线通过前两个力的汇交点.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
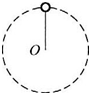
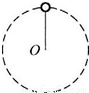
 如图所示,一轻绳一端固定质量为m的小球,以另一端O为圆心使小球在竖直平面内作半径为R的圆周运动,重力加速度为g,则下列说法中正确的是( )
如图所示,一轻绳一端固定质量为m的小球,以另一端O为圆心使小球在竖直平面内作半径为R的圆周运动,重力加速度为g,则下列说法中正确的是( )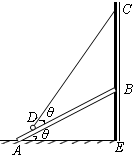 如图所示,一轻绳一端悬于墙面上C点,另一端拴一重为
如图所示,一轻绳一端悬于墙面上C点,另一端拴一重为