题目内容
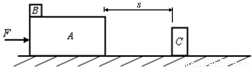
如图所示，水平支持面上静止叠放长方体物块A和B，A的长度为L=2m、高度h=0.8m，B的大小可以忽略，并置于A的左端。在距离A的右端一定距离（用S表示）的地方固定另一个长方体物体C，它的高度为A高的四分之三、长度为A长的五分之一。现对A作用一个水平恒力F，使A、B一起向C运动。已知A、B之间的最大静摩擦力为
N，A、B以及A与地面间的动摩擦因数均为
， A、B的质量分别为
kg、
kg。如果A在运动过程中与C发生碰撞，它将在碰撞后立即停止运动。
（1）为了保证B物体能在A、C发生碰撞后离开A的上表面，应使A、C之间的距离S至少多大？
（2）现使S等于（1）中所求值的两倍，为了保证B物体在A碰到C后能够不碰到C而直接落于水平支持面，求恒力F的最短作用时间；
（3）在S等于（1）中所求值两倍的条件下，计算B物体平抛运动中水平支持面上落点离A右端距离的范围。
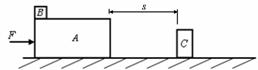
（1）
用
表示所求最小距离
…………（1分）
得
……………（1分）
计算得到
…………（1分）
（3）
…………（1分）
以上两式共1分
…………（1分）
而由（2）中计算得
所以
…………（1分）
……………（1分）
练习册系列答案
阅读快车系列答案
相关题目
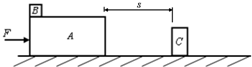如图所示，水平支持面上静止叠放长方体物块A和B，A的长度为L=2m、高度h=0.8m，B的大小可以忽略，并置于A的左端．在距离A的右端一定距离（用S表示）的地方固定另一个长方体物体C，它的高度为A高的四分之三、长度为A长的五分之一．现对A作用一个水平恒力F，使A、B一起向C运动．已知A、B之间的最大静摩擦力为fm=25N，A、B以及A与地面间的动摩擦因数均为μ=0.4，A、B的质量分别为mA=10kg、mB=5kg．如果A在运动过程中与C发生碰撞，它将在碰撞后立即停止运动．
