质量相等的均质柔软细绳A.B平放于水平地面.绳A较长.现分别捏住两绳的中点将绳缓慢提起.直至全部离开地面．已知两绳的中点被提升的高度分别为hA.hB.提升过程中克服重力做功分别为WA.WB．则( )A．若hA=hB.则可能有WA=WBB．若hA＞hB.则可能有WA＜WBC．若hA＜hB.则一定有WA＜WBD．若hA＞hB.则一定有WA＞WB 题目和参考答案——青夏教育精英家教网—

题目内容

5．质量相等的均质柔软细绳A、B平放于水平地面，绳A较长，现分别捏住两绳的中点将绳缓慢提起，直至全部离开地面．已知两绳的中点被提升的高度分别为h_A、h_B，提升过程中克服重力做功分别为W_A、W_B．则（　　）

	A．	若h_A=h_B，则可能有W_A=W_B		B．	若h_A＞h_B，则可能有W_A＜W_B
	C．	若h_A＜h_B，则一定有W_A＜W_B		D．	若h_A＞h_B，则一定有W_A＞W_B

分析质量相等的均质柔软细绳，则长的绳子，其单位长度的质量小，根据细绳的重心上升的高度找出克服重力做功的关系．

解答解：A、两绳中点被提升的高度分别为h_A、h_B，h_A=h_B，绳A较长．所以绳A的重心上升的高度较小，质量相等，所以W_A＜W_B．故A错误
B、h_A＞h_B，绳A较长．所以绳A的重心上升的高度可能较小，质量相等，所以可能W_A＜W_B．故B正确，D错误
C、h_A＜h_B，绳A较长．所以绳A的重心上升的高度一定较小，质量相等，所以W_A＜W_B．故C正确．
故选：BC．

点评解决该题关键要知道柔软细绳不能看成质点，找出不同情况下重心上升的高度的关系．

练习册系列答案

	A．	落地时动能相同		B．	落地时动量相同
	C．	下落过程重力的冲量相同		D．	在任意1s内的动量的变化相同

16．如图所示，是测量两节干电池组成的串联电池组的电动势和内阻的实验所用器材，用实线将他们连接起来

13．正在运动着的物体，如果它所受的一切外力同时消失，那么它将（　　）

	A．	立即停下来		B．	先慢下来，然后再停下来
	C．	改变运动方向		D．	沿原来的运动方向做匀速直线运动

20．（1）关于《互成角度的两个共点力的合成》的实验中，所需的器材除方木板、两个细绳套、两只弹簧秤、铅笔、刻度尺、三角板，还需要器材是白纸，橡皮条，图钉．
（2）做《互成角度的两个共点力合成》的实验时，主要应进行步骤是：
①把木板平放在桌面上，再用图钉把白纸钉在木板上；
②只用一只弹簧秤通过细绳套把橡皮条拉到O点，记下弹簧秤的读数和细绳的方向，按选定的标度作出这个力F′的图示；
③记下两个弹簧秤的读数，描下像皮条和两个细绳的方向及结点的位置O；
④比较F′和F的大小和方向是否相同；
⑤用图钉把橡皮条的一端固定在板上的A点，另一端拴上两个细绳套；
⑥用两个弹簧秤分别钩住细绳套，互成角度地拉橡皮条，使结点到达某一位置O；
⑦在白纸上按选定的标度作出两个力F₁和F₂的图示，并以F₁和F₂为邻边利用三角板和刻度尺作平行四边形，过O点作对角线，作出合力F的图示．
上述步骤中，其正确的完成顺序按序号排列应为①⑤⑥③⑦②④．

10．

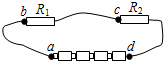如图所示，四节干电池与两个电阻串联组成电路，三根导线中有一根是断的，另外两根导线、电池、电阻R₁、R₂都是好的．将多用电表的红表笔接在电源的正极a，黑表笔依次接在b、c、d三点，通过观察多用电表的示数，查出了这根断导线，则应选择多用电表的（　　）

17．如图所示的情形中，不涉及牛顿第三定律的有（　　）

	A．	气垫船旋转的螺旋浆获得动力		B．	战斗机在行进途中抛弃副油箱
	C．	玩具火箭靠喷出火药飞上天空		D．	喷水龙头自动旋转使喷水均匀

10．

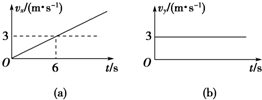快艇要从岸边某一不确定位置处到达河中离岸边100m远的一固定浮标处，已知快艇在静水中的速度v_x与时间t图象和流水的速度v_y与时间t图象如图所示，则（　　）

	A．	快艇的运动轨迹为直线
	B．	快艇的运动轨迹为曲线
	C．	能找到某一位置使其以最快到达浮标处的时间为10s
	D．	最快到达浮标经过的位移为100 m

11．如图所示，A、B二物体从O点开始运动，从A、B二物体的位移图象可知，下述说法中正确的是（　　）

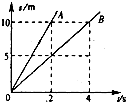
	A．	A、B二物体的运动方向相同		B．	A物体2s内发生的位移是10m
	C．	B物体发生10m的位移的时间是2s		D．	A、B两物体同时运动

试题分类