题目内容
18.在匀强电场中,将质子和α粒子由静止释放,若不计重力,当它们获得相同动能时,质子经历的时间t1和α粒子经历的时间t2之比为( )| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
分析 由牛顿第二定律求出加速度,由速度公式求出粒子的速度,然后根据粒子动能相等求出粒子的运动时间之比.
解答 解:粒子的加速度:a=$\frac{qE}{m}$,
粒子的速度:v=at=$\frac{qEt}{m}$,
粒子的动能:EK=$\frac{1}{2}$mv2=$\frac{{q}^{2}{E}^{2}{t}^{2}}{2m}$,
则时间:t=$\frac{\sqrt{2m{E}_{K}}}{qE}$,
质子经历的时间t1和α粒子经历的时间t2之比:
$\frac{{t}_{1}}{{t}_{2}}$=$\frac{\frac{\sqrt{2m{E}_{K}}}{qE}}{\frac{\sqrt{2×4m{E}_{K}}}{2qE}}$=$\frac{1}{1}$;
故选:A.
点评 本题考查了求时间之比,知道粒子在匀强电场中做匀加速直线运动,应用牛顿第二定律、速度公式与动能的计算公式可以解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.两个共点力的大小分别为5N和8N,其合力可能为( )
| A. | 3.14N | B. | 2N | C. | 14N | D. | 11N |
10.伽利略的理想斜面实验证明了( )
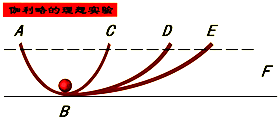

| A. | 要让物体运动必须施加力的作用,没有力的作用时,物体将静止 | |
| B. | 要使物体静止必须有力的作用,没有力的作用时,物体将运动 | |
| C. | 只要物体是运动着的,就必然受到力的作用 | |
| D. | 如果物体不受外力作用时,总会保持原来的静止或匀速直线运动状态. |
7.关于感应电动势的大小,下列说法中正确的是( )
| A. | 磁通量越大,则感应电动势越大 | |
| B. | 磁通量减小,则感应动势一定是减小 | |
| C. | 磁通量增加,感应电动势就增大 | |
| D. | 磁通量变化越快,则感应电动势也越大 |
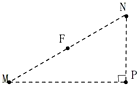 如图的光滑水平面上,在正点电荷Q的电场中有M、N、P、F四点,M、N、P为直角三角形的三个顶点,F为MN的中点,∠M=30°,M、N、P、F四点的电势分别用φM、φN、φP、φF表示.已知φM=φN=2V,φP=φF=4V,
如图的光滑水平面上,在正点电荷Q的电场中有M、N、P、F四点,M、N、P为直角三角形的三个顶点,F为MN的中点,∠M=30°,M、N、P、F四点的电势分别用φM、φN、φP、φF表示.已知φM=φN=2V,φP=φF=4V,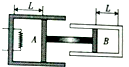 如图所示,结构相同的 汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=5:3,两汽缸内均装有处于平衡状态的某理想气体,开始时汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均为外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强为原来的1.5倍.设环境温度始终不变,求:
如图所示,结构相同的 汽缸A与导热汽缸B均固定于地面,由刚性杆连接的绝热活塞与两汽缸间均无摩擦.已知两汽缸的横截面积之比SA:SB=5:3,两汽缸内均装有处于平衡状态的某理想气体,开始时汽缸中的活塞与缸底的距离均为L,温度均为T0,压强均为外界大气压.缓慢加热A中气体,停止加热达到稳定后,A中气体压强为原来的1.5倍.设环境温度始终不变,求: