题目内容
12.(1)某同学在做“利用单摆测重力加速度”实验中,先测得摆线长L为97.50cm,(如图甲)利用游标卡尺测得摆球直径D为1.150cm,然后用秒表记录了单摆振动50次所用的时间t(如图乙),秒表所示读数为99.8s,则该摆摆长表达式为L+$\frac{D}{2}$.
(2)为提高实验精度,该同学在实验中改变摆长l并测出相应的周期T,得出一组对应的l与T的数据如表所示.
| l/cm | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| T/s | 2.02 | 2.51 | 2.83 | 3.18 | 3.64 | 4.05 |
(3)(单选题)如果他测得的g值偏小,可能的原因是B
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时,秒表过迟按下
D.实验中误将49次全振动数为50次.
分析 (1)单摆的摆长等于摆线的长度与摆球半径之和;秒表先读分针读数,再读秒针读数,两者相加;机械式秒表的小表盘表示分钟,大表盘表示秒,大表盘一圈30秒;为了确定是前三十秒还是后三十秒,需要参考小表盘两分钟之间的半刻线,如果小表盘表针没到半刻线,就是某分钟+小表盘示数秒;如果小表盘表针超过了半刻线,就是某分钟+(大表盘示数+30)秒.
(2)应用描点法作图,根据作出的T2-l图象求出图象的斜率,然后根据单摆周期公式求出重力加速度.
(3)据T2=$\frac{4{π}^{2}L}{g}$分析g的变化.
解答 解:(1)据游标卡尺可知,游标的第10个小格对齐,所以读数为:1.1cm+0.05×10mm=11.50cm.
小表盘表针超过了半刻线,故:t=60s+39.8s=99.8s.
单摆的摆长为:L=l线+$\frac{D}{2}$;
(2)根据表中实验数据,应用描点法作图,T2-l图象如下图所示;由单摆周期公式T=2π$\sqrt{\frac{L}{g}}$可得,
T2=$\frac{4{π}^{2}L}{g}$,
由此可知T2与L成正比,因此T2-L图象斜率k=$\frac{4{π}^{2}}{g}$,由图象可知,图象斜率k=4s2/m,
则重力加速度g=$\frac{4{π}^{2}}{k}$=$\frac{4×3.1{4}^{2}}{4}$m/s2≈9.86m/s2;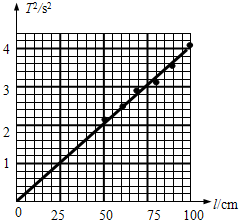
(3)据单摆的周期公式可得:g=$\frac{4{π}^{2}L}{{T}^{2}}$.
A、测摆线时摆线拉得过紧,则摆长的测量量偏大,则测得的重力加速度偏大.故A错误.
B、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,而测得的摆长偏小,则测得重力加速度偏小.故B正确.
C、开始计时,秒表过迟按下,测得单摆的周期偏小,则测得的重力加速度偏大.故C错误.
D、实验中误将49次全振动数为50次.测得周期偏小,则测得的重力加速度偏大.故D错误.
故选:B.
故答案为:(1)1.150;99.8;L+$\frac{D}{2}$;(2)如图所示;9.86;(3)B.
点评 一定要注意单摆摆长是摆线长度与摆球半径之和,摆线的长度不是摆长;本题难度不大,是一道基础题,牢固掌握基础知识、熟练应用单摆周期公式是正确解题的关键.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 水平固定放置的足够长的U形金属导轨处于竖直向上的匀强磁场中,在导轨上放着金属棒ab,开始时ab棒以水平初速度v0向右运动,最后静止在导轨上,就导轨光滑和粗糙两种情况比较,这个过程( )
水平固定放置的足够长的U形金属导轨处于竖直向上的匀强磁场中,在导轨上放着金属棒ab,开始时ab棒以水平初速度v0向右运动,最后静止在导轨上,就导轨光滑和粗糙两种情况比较,这个过程( )| A. | 安培力对ab棒所做的功相等 | B. | 电流所做的功相等 | ||
| C. | 产生的总热量相等 | D. | ab棒的动量改变量相等 |
| A. | 4cm,10cm | B. | 4cm,20cm | C. | 0,24cm | D. | 100cm,100cm |
| A. | 线速度 | B. | 向心加速度 | C. | 角速度 | D. | 向心力 |

 如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上,另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上,当A以O为圆心做半径r=0.2m的匀速圆周运动时,地面对B的支持力FN=3.0N,则物块A的角速度大小为10rad/s.
如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上,另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上,当A以O为圆心做半径r=0.2m的匀速圆周运动时,地面对B的支持力FN=3.0N,则物块A的角速度大小为10rad/s.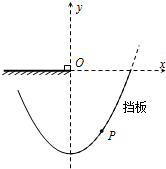 如图所示,一小物块(可看作质点)以v=1m/s的速度从平台边缘O点水平抛出,击中平台右下侧挡板上的P点.以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程y=x2-6(单位:m).取重力加速度g=10m/s2.试求P点的坐标.
如图所示,一小物块(可看作质点)以v=1m/s的速度从平台边缘O点水平抛出,击中平台右下侧挡板上的P点.以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程y=x2-6(单位:m).取重力加速度g=10m/s2.试求P点的坐标.