题目内容
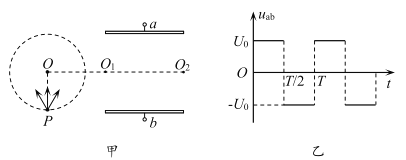
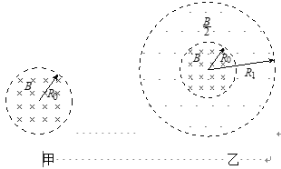
【题目】如图甲所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B。一粒子源置于圆心,在纸面内沿各个方向以相同速率发射大量粒子,所有粒子刚好都不离开磁场。已知粒子的质量为m、电荷量为+q,不考虑粒子之间的相互作用:
(1)求带电粒子的速率v;
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为![]() ,求粒子在磁场中最长的运动时间t;
,求粒子在磁场中最长的运动时间t;
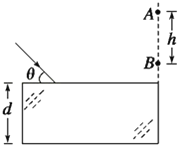
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,如图乙所示,磁场的磁感应强度的大小为![]() ,方向垂直于纸面向外,两磁场区域成同心圆,此时从圆心处的粒子源出发的粒子都能回到圆心,求R1的最小值和粒子运动的周期T。
,方向垂直于纸面向外,两磁场区域成同心圆,此时从圆心处的粒子源出发的粒子都能回到圆心,求R1的最小值和粒子运动的周期T。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)粒子在磁场中做匀速圆周运动,有
![]()

由几何关系得
![]()
解得
![]()
(2)磁场的大小变为![]() 后,设粒子的轨道半径为
后,设粒子的轨道半径为![]() ,由
,由
![]()
解得
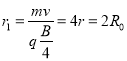
在磁场中轨迹为劣弧,弦长越长,对应圆心角越大,时间越长,则在磁场中最大弦长为![]() ,如图
,如图

圆周轨迹对应的圆心角为![]() ,最长时间
,最长时间
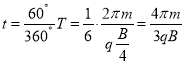
(3)根据磁场的叠加法则可知,垂直纸面向里和垂直纸面向外的磁场大小均为![]() ,可知半径
,可知半径
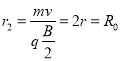
粒子在磁场中运动的轨迹如图
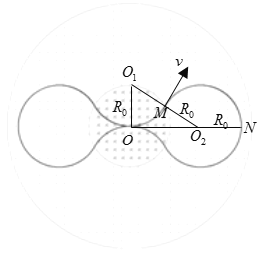
可知![]() 的最小值为
的最小值为![]() 长度,根据几何关系可知
长度,根据几何关系可知
![]()
则
![]()
粒子运动的周期为
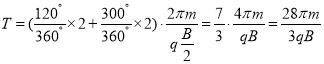

 灵星计算小达人系列答案
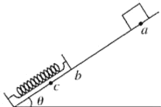
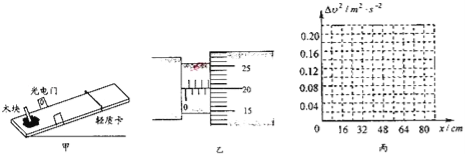
灵星计算小达人系列答案【题目】为测量木块与木板间的动摩擦因数,将木反倾斜,木块以不同的初速度沿木板向上滑到最高点后再返回,用光电门测量木块来回的速度,用刻度尺测量向上运动的最大距离,为确定木块向上运动的最大高度,让木块推动轻质卡到最高点,记录这个位置,实验装置如图甲所示.
(1)本实验中,下列操作合理的是
A.遮光条的宽度应尽量小些 |
B.实验前将轻质卡置于光电门附近 |
C.为了实验成功,木块的倾角必须大于某一值 |
D.光电门与轻质卡最终位置间的距离即为木块向上运动的最大距离 |
(2)用螺旋测微器测量遮光条的宽度,如图乙所示读数为 mm.
(3)改变木块的初速度,测量出它向上运动的最大距离与木块来回经过光电门时速度的平方差,结果如下表所示,试在丙图坐标纸上作出△v2﹣x的图象,经测量木板倾角的余弦值为0.6,重力加速度取g=9.80m/s2,则木块与木板间的动摩擦因数为 (结果保留两位有效数字).
序号 | 1 | 2 | 3 | 4 | 5 |
X/cm | 16.0 | 36.0 | 60.0 | 70.0 | 88.0 |
△v2/m2s﹣2 | 0.04 | 0.09 | 0.15 | 0.19 | 0.22 |
(4)由于轻质卡的影响,使得测量的结果 (选填“偏大”或“偏小”).