题目内容
5.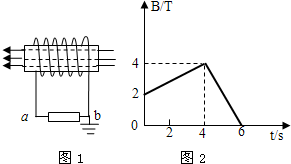 如图1所示的一个螺线管,匝数n=1000,横截面积为S=200cm2,电阻r=1Ω,在螺线管外接一个阻值R=4Ω的电阻,电阻的一端b跟地相接.一方向向左,穿过螺线管的匀强磁场的磁感应强度随时间变化规律如图2线B-t所示,求:
如图1所示的一个螺线管,匝数n=1000,横截面积为S=200cm2,电阻r=1Ω,在螺线管外接一个阻值R=4Ω的电阻,电阻的一端b跟地相接.一方向向左,穿过螺线管的匀强磁场的磁感应强度随时间变化规律如图2线B-t所示,求:(1)从计时起在t=3s、t=5s时穿过螺线管的磁通量是多少?
(2)在前6s内电阻R产生的热量.
分析 (1)根据磁场与时间变化的图象,可知在t1=3s、t2=5s时磁感应强度,再由∅=BS,即可求解;
(2)由法拉第电磁感应定律,求得各段感应电动势的大小,再结合焦耳定律,即可求解.
解答 解:(1)t1=3s、t2=5s时磁感应强度分别为:
B1=3.5T、B2=2T,
则这两个时刻的磁通量分别为
Φ1=B1•S磁场=3.5×200×10-4=7.0×10-2Wb,
Φ2=B2•S磁场=2×200×10-4=4.0×10-2Wb.
(2)在0~4s内,根据法拉第电磁感应定律,则有,
E1=N$\frac{△B•S}{△t}$=1000×0.5×200×10-4V=10V
根据焦耳定律,则有,在0~4s内产生热量Q1=$\frac{{E}_{1}^{2}}{R+r}{t}_{1}$=$\frac{1{0}^{2}}{4+1}×4$=80J
在4~6s内,则有,E2=N$\frac{△B′•S}{△t}$=1000×2×200×10-4V=40V
根据焦耳定律,则有,在4~6s内产生热量Q2=$\frac{{E}_{2}^{2}}{R+r}{t}_{2}$=$\frac{4{0}^{2}}{5}×2$=640J
因此前6s内电阻R产生的热量Q=80+640=720J
答:(1)从计时起在t1=3s、t2=5s时穿过线圈的磁通量分别是7.0×10-2Wb,4.0×10-2Wb.
(2)前6s内电阻R产生的热量720J.
点评 考查如何读懂图象,掌握磁通量表达式,理解法拉第电磁感应定律的应用,及掌握焦耳定律的应用,分段求得热量是解题的注意点.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.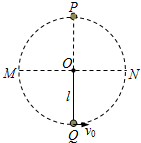 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
 “水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )
“水流星”是一种常见的杂技项目,该运动可以简化为轻绳一端系着小球在竖直平面内的圆周运动模型,如图所示,已知绳长为l,重力加速度为g,忽略空气阻力,则( )| A. | 小球运动到最低点Q时,处于超重状态 | |
| B. | 小球初速度v0越大,则在P、Q两点绳对小球的拉力差越大 | |
| C. | 当v0>$\sqrt{6gl}$,小球一定能通过最高点P | |
| D. | 当v0<$\sqrt{gl}$,细绳始终处于绷紧状态 |
20.一按正弦规律变化的交流电的图象如图所示,根据图象可知( )


| A. | 该交流电电压的有效值是14.1V | |
| B. | 该交流电的电压瞬时值表达式是u=20sin0.02t (V) | |
| C. | 在t=$\frac{T}{8}$(T为交流电的周期)时,该电压的大小与其有效值相等 | |
| D. | 使用这个交流电的用电器,每通过1C的电量时,电流做了14.1J的功 |
10. 在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
 在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )
在半径为R的圆形区域内有磁感应强度为B的匀强磁场,一个电子(电荷量为e,质量为m)从M点沿半径方向以速度v0射入,从N点射出时的速度方向偏转了60°,如图则电子从M到N运行的时间是( )| A. | $\frac{πm}{3eB}$ | B. | $\frac{πm}{6eB}$ | C. | 、$\frac{πR}{{3{v_0}}}$ | D. | $\frac{{\sqrt{3}πR}}{{3{v_0}}}$ |
 如图所示,在xOy坐标系的第一象限里有平行于坐标平面向右的匀强电场,在第四象限有平行于坐标平面向上的匀强电场,两个电场的场强大小相等,同时在第四象限还有垂直于坐标平面的匀强磁场(图中未画出),一带电小球从坐标原点O,以与x轴正向成45°向上的初速度v0射入第一象限的电场,已知小球的质量为m,带电荷量为+q,电场的场强大小E=$\frac{mg}{q}$,小球在第四象限中运动,恰好不能进入第三象限,求:
如图所示,在xOy坐标系的第一象限里有平行于坐标平面向右的匀强电场,在第四象限有平行于坐标平面向上的匀强电场,两个电场的场强大小相等,同时在第四象限还有垂直于坐标平面的匀强磁场(图中未画出),一带电小球从坐标原点O,以与x轴正向成45°向上的初速度v0射入第一象限的电场,已知小球的质量为m,带电荷量为+q,电场的场强大小E=$\frac{mg}{q}$,小球在第四象限中运动,恰好不能进入第三象限,求: