题目内容
 如图所示,有一磁感应强度B=9.1×10-4 T的匀强磁场,C、D为垂直于磁场方向的一平面内的两点,今有一电子在此磁场中运动,它经过C点时速度v的方向和磁场垂直,且与CD之间的夹角θ=30°,电子在运动中后来又经过D点,则电子从C点第一次到D点所用的时间是
如图所示,有一磁感应强度B=9.1×10-4 T的匀强磁场,C、D为垂直于磁场方向的一平面内的两点,今有一电子在此磁场中运动,它经过C点时速度v的方向和磁场垂直,且与CD之间的夹角θ=30°,电子在运动中后来又经过D点,则电子从C点第一次到D点所用的时间是6.5×10-9
6.5×10-9
s.(me=9.1×10-31kg,e=1.6×10-19C)分析:过C点作垂直速度v的直线CO、作弦CD的中垂线交CO于O点,则O即为电子做匀速圆周运动的圆心;根据几何关系求出电子运动的圆心角α=60°,然后根据公式t=
?
求运动时间.
| θ |
| 2π |
| 2πm |
| qB |
解答:解:作出粒子做圆周运动的轨迹如图所示.
 .
.
由几何知识得:轨迹的圆心角为2θ=60°,
故电子由C到D运动时间t=
=
×
=
×
=6.5×10-9s.
故答案为:6.5×10-9s.
 .
.由几何知识得:轨迹的圆心角为2θ=60°,
故电子由C到D运动时间t=
| T |
| 6 |
| 1 |
| 6 |
| 2πm |
| qB |
| 1 |
| 3 |
| 3.14×9.1×10-31 |
| 1.6×10-19×9.1×10-4 |
故答案为:6.5×10-9s.
点评:求解带电粒子在匀强磁场中做匀速圆周运动的力学问题,根据速度方向一定垂直于轨迹半径、弦的中垂线一定通过圆心,正确地找出圆心、画出圆运动的轨迹是解题过程中要做好的第一步.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
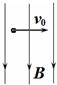 如图所示,有一磁感应强度为B,方向竖直向下的匀强磁场,一束电子流以初速度v0从水平方向射入,为了使电子流经过磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,这个电场的方向大小和方向是( )
如图所示,有一磁感应强度为B,方向竖直向下的匀强磁场,一束电子流以初速度v0从水平方向射入,为了使电子流经过磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,这个电场的方向大小和方向是( )A、
| ||
B、
| ||
| C、B?v0,垂直纸面向外 | ||
| D、B?v0,垂直纸面向里 |
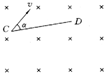 如图所示,有一磁感应强度B=9.1×10-4T的匀强磁场,C、D为垂直于磁场的同一平面内的两点,它们之间的距离l=0.05m,今有一电子在此磁场中运动,它经过C点时的速度v的方向和磁场方向垂直,且与CD间的夹角α=30°,问:
如图所示,有一磁感应强度B=9.1×10-4T的匀强磁场,C、D为垂直于磁场的同一平面内的两点,它们之间的距离l=0.05m,今有一电子在此磁场中运动,它经过C点时的速度v的方向和磁场方向垂直,且与CD间的夹角α=30°,问:
