题目内容
如图所示,半径R="0.5" m的光滑半圆轨道竖直固定在高h="0.8" m的光滑水平台上,与平台平滑连接,平台长L="1.2" m.可视为质点的两物块m1、m2紧靠在一起静止在平台的最右端D点,它们之间有烈性炸药.今点燃炸药,假设炸药释放出来的能量全部转化为物块m1、m2的机械能,使它们具有水平方向的速度,m1通过平台到达半圆轨道的最高点A时,轨道对它的压力大小是N="44" N,水平抛出落在水平地面上的P点,m2也落在P点,已知m1="2" kg,g取10 m/s2.求炸药释放出来的能量是多少?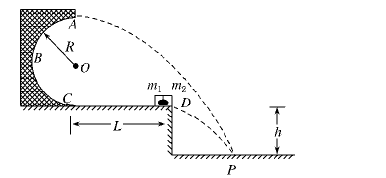
54 J
设m1在A点时的速度为v,由牛顿第二定律得mg+N=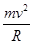
,
有v=4 m/s
从A点到P点运动的时间为t1,
h+2R=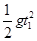
,有t1="0.6" s
设运动的水平距离为s,则s+L=vt1,
故s="1.2" m
设刚爆炸后,m1的速度为v1,由机械能守恒定律得
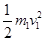=m1g×2R+
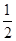m1v2,
解得v1=6 m/s
设平抛时的速度为v2,平抛运动的时间为t2
因h=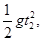
得t2="4" s,
v2=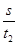
=3 m/s.
对m1、m2爆炸过程运用动量守恒定律得
0=m1v1-m2v2,
所以m2=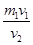
="4" kg
炸药释放出来的能量
E=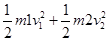
="54" J.
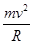,有v=4 m/s
从A点到P点运动的时间为t1,
h+2R=
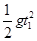,有t1="0.6" s设运动的水平距离为s,则s+L=vt1,
故s="1.2" m
设刚爆炸后,m1的速度为v1,由机械能守恒定律得
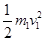=m1g×2R+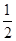m1v2,解得v1=6 m/s
设平抛时的速度为v2,平抛运动的时间为t2
因h=
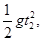
得t2="4" s,
v2=
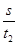=3 m/s.对m1、m2爆炸过程运用动量守恒定律得
0=m1v1-m2v2,
所以m2=
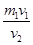="4" kg炸药释放出来的能量
E=
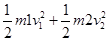="54" J.
练习册系列答案
相关题目
