题目内容
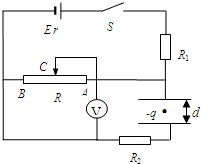 如图所示电路,电源电动势E=90V,内阻r=5Ω,R1=10Ω,R2=20Ω,板面水平放置的平行板电容器的两极板M、N相距d=3cm,在两板间的正中央有一带电液滴,电量q=2×10-7C,质量m=4×10-5kg,取g=10m/s2,求:
如图所示电路,电源电动势E=90V,内阻r=5Ω,R1=10Ω,R2=20Ω,板面水平放置的平行板电容器的两极板M、N相距d=3cm,在两板间的正中央有一带电液滴,电量q=2×10-7C,质量m=4×10-5kg,取g=10m/s2,求:(1)若液滴恰好能处于静止状态,电压表的示数是多少?若此时滑动变阻器的滑动触头C正好在变阻器正中点,那么滑动变阻器的最大阻值Rm是多大?
(2)将滑动触头C迅速滑到A端,则液滴将向哪个极板作什么性质的运动?到达该极板时的速度是多大?
分析:(1)根据二力平衡,液滴的电场力等于重力,从而求出电压;
(2)将滑动触头C迅速滑到A端,看似是含有滑动变阻器的问题,实则可以使用闭合电路的欧姆定律来解题.求出电压表上的电压后即可判断则液滴将向哪个极板作什么性质的运动,以及达到极板的速度.
(2)将滑动触头C迅速滑到A端,看似是含有滑动变阻器的问题,实则可以使用闭合电路的欧姆定律来解题.求出电压表上的电压后即可判断则液滴将向哪个极板作什么性质的运动,以及达到极板的速度.
解答:解:(1)液滴静止,则有:q
=mg
得:UC1=
=60V 电压表示数为60V
电路中的电流为:I1=
=2A
则:
=
代人数据,解得:Rm=60Ω
(2)液滴向上做加速直线运动,此时电容器两端电压为:
UC2=
?Rm=72V
设粒子达到极板的速度是v,由动能定理:
q
-mg
=
mv2-0
代人数据得:v=
m/s
答:
(1)液滴静止时,电压表的示数是60V,滑动变阻器的最大阻值60Ω;
(2)液滴向上做加速直线运动,到达该极板时的速度是
m/s
| UC1 |
| d |
得:UC1=
| mgd |
| q |
电路中的电流为:I1=
| E-UC1 |
| (R1+r) |
则:
| Rm |
| 2 |
| UC1 |
| I1 |
代人数据,解得:Rm=60Ω
(2)液滴向上做加速直线运动,此时电容器两端电压为:
UC2=
| E |
| R1+Rm+r |
设粒子达到极板的速度是v,由动能定理:
q
| UC2 |
| 2 |
| d |
| 2 |
| 1 |
| 2 |
代人数据得:v=
| ||
| 10 |
答:
(1)液滴静止时,电压表的示数是60V,滑动变阻器的最大阻值60Ω;
(2)液滴向上做加速直线运动,到达该极板时的速度是
| ||
| 10 |
点评:该题考查到电场中液滴的受力平衡与闭合电路的欧姆定律,属于该部分知识的基本应用.公式虽然较多,思路还是比较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示电路,电源电压不变,已知:电阻R1的电阻值为1Ω,电阻R2的阻值为3Ω,则电流表 1 和电流表 2 的示数比为( )
如图所示电路,电源电压不变,已知:电阻R1的电阻值为1Ω,电阻R2的阻值为3Ω,则电流表 1 和电流表 2 的示数比为( ) 如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( )
如图所示电路,电源电动势为E,内阻为r,Rt为光敏电阻(光照强度增加时,其电阻值减小).现增加光照强度,则下列判断正确的是( ) 如图所示电路,电源电动势E=12.0V,内电阻r=2.0Ω,R1=40Ω,R2=20Ω,R3=12Ω,R4=10Ω.电压表和电流表都是理想电表.图中两电表示数各是多大?
如图所示电路,电源电动势E=12.0V,内电阻r=2.0Ω,R1=40Ω,R2=20Ω,R3=12Ω,R4=10Ω.电压表和电流表都是理想电表.图中两电表示数各是多大?
