题目内容
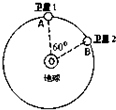 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.计划“北斗”系统最终将有5颗静止轨道卫星和30颗非静止轨道卫星组成.这些卫星均绕地心O做匀速圆周运动.某时刻两颗正在同时提供服务的非静止轨道卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,轨道半径为r,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中错误的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.计划“北斗”系统最终将有5颗静止轨道卫星和30颗非静止轨道卫星组成.这些卫星均绕地心O做匀速圆周运动.某时刻两颗正在同时提供服务的非静止轨道卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,轨道半径为r,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中错误的是( )A、这两颗卫星的加速度大小相等,均为
| ||||||
B、卫星1由位置A运动到位置B所需的时间为
| ||||||
| C、卫星1由位置A运动到位置B的过程中万有引力做功为零 | ||||||
| D、卫星1向后喷气就一定能追上卫星2 |
分析:由
=
=
可得出r相同则速度v大小相等,v变大则r变大(做离心运动),再结合
=mg即GM=gR2(黄金代换),即可求解.
| GMm |
| r2 |
| m?4π2r |
| T2 |
| mv2 |
| r |
| GMm |
| R2 |
解答:解:A、根据F合=ma得,对卫星有
=ma,
加速度a=
,
根据地球表面物体万有引力等于重力得:
=mg,即GM=gR2
联立解得a=
所以这两颗卫星的加速度大小相等,均为
.故A正确;
B、根据
=
得
T=2π
①
GM=gR2②
t=
T③
联立①②③可解得t=
,故B正确;
C、卫星1由位置A运动到位置B的过程中,由于万有引力始终与速度垂直,故万有引力不做功,故C正确;
D、若卫星1向后喷气,则其速度会增大,卫星1将做离心运动,所以卫星1不可能追上卫星2.故D错误
本题选错误的,故选:D.
| GMm |
| r2 |
加速度a=
| GM |
| r2 |
根据地球表面物体万有引力等于重力得:
| GMm |
| R2 |
联立解得a=
| R2g |
| r2 |
所以这两颗卫星的加速度大小相等,均为
| R2g |
| r2 |
B、根据
| GMm |
| r2 |
| m?4π2r |
| T2 |
T=2π
|
GM=gR2②
t=
| 1 |
| 6 |
联立①②③可解得t=
| πr |
| 3R |
|
C、卫星1由位置A运动到位置B的过程中,由于万有引力始终与速度垂直,故万有引力不做功,故C正确;
D、若卫星1向后喷气,则其速度会增大,卫星1将做离心运动,所以卫星1不可能追上卫星2.故D错误
本题选错误的,故选:D.
点评:关于做圆周运动的卫星类问题,要灵活运用两个公式
=
=
,
=mg,注意卫星若加速则做离心运动,减速则做向心运动.
| GMm |
| r2 |
| m?4π2r |
| T2 |
| mv2 |
| r |
| GMm |
| R2 |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
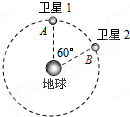 2012年我国宣布北斗导航系统正式商业运行.北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星均绕地心做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中正确的是( )
2012年我国宣布北斗导航系统正式商业运行.北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星均绕地心做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中正确的是( ) (2011?开封二模)北斗导航系统又被称为“双星定位系统”,具有导航,定位等功能.“北斗”系统中两颗工作卫星均围绕地心做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中错误的是( )
(2011?开封二模)北斗导航系统又被称为“双星定位系统”,具有导航,定位等功能.“北斗”系统中两颗工作卫星均围绕地心做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中错误的是( )