题目内容
19. 如图所示,内壁光滑的圆锥筒固定不动,其轴线OO′垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在水平面内绕轴线OO′做匀速圆周运动,则下列说法中正确的是( )
如图所示,内壁光滑的圆锥筒固定不动,其轴线OO′垂直于水平面,两个质量相同的小球A和B紧贴着内壁分别在水平面内绕轴线OO′做匀速圆周运动,则下列说法中正确的是( )| A. | 球A的角速度大于B球的角速度 | |
| B. | 球A的线速度大于B球的线速度 | |
| C. | 球A的向心加速度等于球B的向心加速度 | |
| D. | 球A对侧壁的压大于球B对侧壁的压力 |
分析 小球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据牛顿第二定律得出角速度、向心加速度的表达式,从而比较大小,根据平行四边形定则求出支持力的大小,从而比较压力的大小.
解答 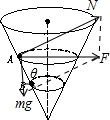 解:A、对小球受力分析,小球受到重力和支持力,它们的合力提供向心力,如图,根据牛顿第二定律,有:
解:A、对小球受力分析,小球受到重力和支持力,它们的合力提供向心力,如图,根据牛顿第二定律,有:
F=mgtanθ=ma=mrω2=$m\frac{{v}^{2}}{r}$,解得a=gtanθ,$ω=\sqrt{\frac{gtanθ}{r}}$,v=$\sqrt{grtanθ}$,A的半径大,角速度小,线速度大,向心加速度相等.故A错误,B正确,C正确.
D、根据平行四边形定则知,N=$\frac{mg}{cosθ}$,可知支持力大小相等,则球A对侧壁的压力与球B对侧壁的压力大小相等,故D错误.
故选:BC.
点评 解决本题的关键知道圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
10.图中的实线表示电场线,虚线表示只受电场力作用的带电粒子的运动轨迹,可以判定( )


| A. | 若粒子带负电,其运动是从M点运动到N点 | |
| B. | 粒子只能是带正电,它在M点的电势能大于在N点的电势能 | |
| C. | 粒子从M运动到N过程,电势能转化为粒子的动能 | |
| D. | 粒子在M点的加速度小于它在N点的加速度 |
7.铅蓄电池的电动势为2V,这表示( )
| A. | 电路中每通过1 C电荷量,电源把2 J的化学能转变为电能 | |
| B. | 无论接不接入外电路,蓄电池两极间的电压都为2 V | |
| C. | 蓄电池在1 s内将2 J的化学能转变为电能 | |
| D. | 蓄电池将化学能转变为电能的本领比一节干电池(电动势为1.5 V)的大 |
14. (1)橡皮筋也像弹簧一样,伸长量与弹力成正比关系,即F=KX,K的值与弹簧没有受力时的长度L和横截面积S有关.理论和实验都表明K=YS/K.其中Y是由材料决定的一个常数,材料力学上称为杨氏模量.
(1)橡皮筋也像弹簧一样,伸长量与弹力成正比关系,即F=KX,K的值与弹簧没有受力时的长度L和横截面积S有关.理论和实验都表明K=YS/K.其中Y是由材料决定的一个常数,材料力学上称为杨氏模量.
①在国际单位中,杨氏模量Y的单位应该是D.
A.N B.m
C.N/m D.Pa
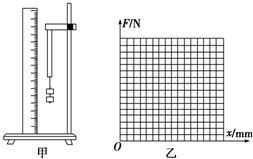
②有一段横截面积是圆形的橡皮筋,应用如图甲所示的实验装置可以测量出它的杨氏模量Y的值.首先利用测量工具a测得橡皮筋的长度L=20.00cm,利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm,用如图甲所示的装置就可以测出这种橡皮筋的Y值,下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.
由此可求得该橡皮筋的劲度系数k=310N/m,这种橡皮筋的杨氏模量Y=5×106.(保留一位有效数字)
 (1)橡皮筋也像弹簧一样,伸长量与弹力成正比关系,即F=KX,K的值与弹簧没有受力时的长度L和横截面积S有关.理论和实验都表明K=YS/K.其中Y是由材料决定的一个常数,材料力学上称为杨氏模量.
(1)橡皮筋也像弹簧一样,伸长量与弹力成正比关系,即F=KX,K的值与弹簧没有受力时的长度L和横截面积S有关.理论和实验都表明K=YS/K.其中Y是由材料决定的一个常数,材料力学上称为杨氏模量.①在国际单位中,杨氏模量Y的单位应该是D.
A.N B.m
C.N/m D.Pa
②有一段横截面积是圆形的橡皮筋,应用如图甲所示的实验装置可以测量出它的杨氏模量Y的值.首先利用测量工具a测得橡皮筋的长度L=20.00cm,利用测量工具b测得橡皮筋未受到拉力时的直径D=4.000mm,用如图甲所示的装置就可以测出这种橡皮筋的Y值,下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.
| 拉力F(N) | 5 | 10 | 15 | 20 | 25 |
| 伸长量x(cm) | 1.6 | 3.2 | 4.8 | 6.4 | 8.0 |
11.下列说法正确的是( )
| A. | 若一小段通电导线在某处不受磁场力作用,则该处磁感应强度一定为零 | |
| B. | 一个带电粒子在某点不受电场力的作用,该点的电场强度一定为零 | |
| C. | 一个带电粒子在磁场中不受磁场的作用力,一定是该粒子不运动 | |
| D. | 一个带电粒子在磁场中受到磁场的作用力不一定与磁场方向垂直 |
9.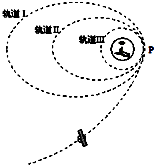 2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探究.不考虑卫星质量变化,下列说法正确的是( )
2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探究.不考虑卫星质量变化,下列说法正确的是( )
 2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探究.不考虑卫星质量变化,下列说法正确的是( )
2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探究.不考虑卫星质量变化,下列说法正确的是( )| A. | 卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度大 | |
| B. | 卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 | |
| C. | 卫星在轨道Ⅲ上过P点时加速度可能比在轨道Ⅰ上过P点时大 | |
| D. | 卫星在轨道Ⅰ上的机械能比在轨道Ⅱ上多 |
 如图所示,电灯的重力为G=10N,AO绳与顶板间的夹角为θ=60°,BO绳水平,则AO绳所受的拉力FA和BO绳所受的拉力FB分别为多少?
如图所示,电灯的重力为G=10N,AO绳与顶板间的夹角为θ=60°,BO绳水平,则AO绳所受的拉力FA和BO绳所受的拉力FB分别为多少?


