Question

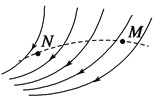
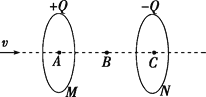
【题目】如图所示，M、N为两个等大的均匀带电圆环，其圆心分别为A、C，带电量分别为＋Q、－Q，将它们平行放置，A、C连线垂直于圆环平面，B为AC的中点，现有质量为m、带电量为＋q的微粒（重力不计）从左方沿A、C连线方向射入，到A点时速度vA＝1 m/s，到B点时速度vB＝m/s，则（ ）

A. 微粒从B至C做加速运动，且vC＝3 m/s

B. 微粒从A到C先做减速运动，后做加速运动

C. 微粒最终可能返回至B点，其速度大小为 m/s

D. 微粒在整个运动过程中的最终速度为 m/s

Answer 1

【答案】AD

【解析】

由图可以知道AC之间电场是对称的，A到B的功和B到C的功相同，依据动能定理可求微粒在C点的速度；过B做垂直AC的线，此线为等势面，微粒出C之后，依据能量守恒可以得到微粒最终的速度应该与B点相同。

AC之间电场是对称的，A到B的功和B到C的功相同，依据动能定理可得：qd＝mvB2mvA2，2qd＝mvC2mvA2，解得：vC=3m/s。故A正确。在到达A点之前，微粒做减速运动，而从A到C微粒一直做加速运动，从C到无穷远处做减速运动，故B错误。过B做垂直AC的线，此线为等势面，微粒出C之后，会向无穷远处运动，而无穷远处电势为零，故B点的动能等于无穷远处的动能，依据能量守恒可以得到微粒最终的速度应该与B点相同，故C错误，D正确。故选AD。