题目内容
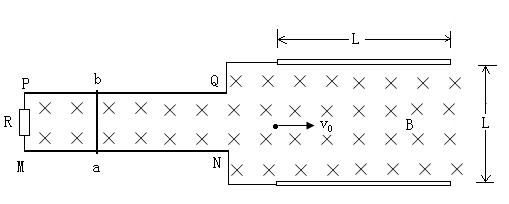
如图所示,![]() 、
、![]() 为一对固定的平行金属导轨,其电阻忽略不计。导轨左端连接一定值电阻
为一对固定的平行金属导轨,其电阻忽略不计。导轨左端连接一定值电阻![]() ,右端通过导线连接着一对固定的平行金属板,金属板板长和板间距离均为
,右端通过导线连接着一对固定的平行金属板,金属板板长和板间距离均为![]() ,且金属板间距离恰好是两导轨间距离的
,且金属板间距离恰好是两导轨间距离的![]() 倍。导轨和金属板间存在方向垂直纸面向里,磁感应强度大小未知的匀强磁场。金属板左端正中间处有一电子源,不断地沿水平向右方向发射速率恒为
倍。导轨和金属板间存在方向垂直纸面向里,磁感应强度大小未知的匀强磁场。金属板左端正中间处有一电子源,不断地沿水平向右方向发射速率恒为![]() 的电子,电子恰好沿下极板右端飞出。为保证电子沿水平方向运动,可在导轨上加一轻质金属杆
的电子,电子恰好沿下极板右端飞出。为保证电子沿水平方向运动,可在导轨上加一轻质金属杆![]() ,其阻值为
,其阻值为![]() ,使其在金属导轨上无摩擦的左右滑动。已知电子的质量为
,使其在金属导轨上无摩擦的左右滑动。已知电子的质量为![]() ,电量为
,电量为![]() ,不考虑电子的重力及电子间的的相互作用。
,不考虑电子的重力及电子间的的相互作用。
(1)为使电子沿水平方向运动,请定性描述金属杆![]() 的运动情况;
的运动情况;
(2)使金属杆ab保持上述的速度运动,则作用在杆上的拉力做功的功率为多大?
(1)见解析(2)![]()
解析:
(1)由左手定则判断出,电子在磁场中运动时受到的洛仑兹力方向竖直向下;要使其沿水平方向飞出磁场,金属板间需有一匀强电场,且上板带正电,下板带负电;从图中可以看出,金属板间的电压与定值电阻![]() 两端电压相等,由右手定则可以判断出,金属杆
两端电压相等,由右手定则可以判断出,金属杆![]() 应该水平向右做匀速直线运动。(5分)
应该水平向右做匀速直线运动。(5分)
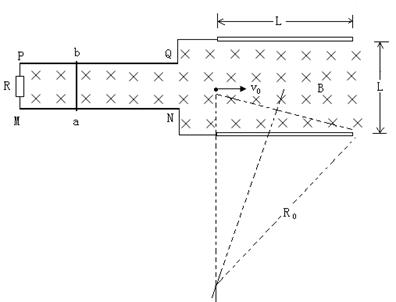
(2)设匀强磁场的磁感应强度为![]() ,没有金属杆时,电子做匀速率圆周运动,设其运动轨道半径为
,没有金属杆时,电子做匀速率圆周运动,设其运动轨道半径为![]() ,如图所示。
,如图所示。
洛仑兹力提供向心力,有:
![]() ① (2分)
① (2分)
由图中几何条件可知:
![]() ② (2分)
② (2分)
联立两式求解得:![]() (1分)
(1分)
设电子水平匀速运动时,两板间的电压为![]() ,根据电子的运动情况有:
,根据电子的运动情况有:
![]() ③ (1分)
③ (1分)
得: ![]() (1分)
(1分)
设金属杆运动速率为![]() , 切割磁感线产生的感应电动势大小为
, 切割磁感线产生的感应电动势大小为![]() ,电流强度为
,电流强度为![]()
由电路可知:
![]() ④ (1分)
④ (1分)
由闭合电路欧姆定律有:
![]() ⑤ (1分)
⑤ (1分)
而:![]() ⑥ (1分)
⑥ (1分)
联立以上三式求解得:![]() ,
,![]() (1分)
(1分)
设作用在杆上的拉力的大小为![]() ,所求功率为
,所求功率为![]() ,则有:
,则有:
![]() ⑦ (1分)
⑦ (1分)
![]() ⑧ (1分)
⑧ (1分)
![]() ⑨ (1分)
⑨ (1分)
联立以上三式求解得:![]() (1分)
(1分)
