题目内容
13.如图甲所示,在倾角为37°的粗糙斜面的底端,一质量m=1kg可视为质点的滑块压缩一轻弹簧并锁定,滑块与弹簧不相连.t=0时解除锁定,计算机通过传感器描绘出滑块的速度时间图象如图乙所示,其中bc段为直线,g取10m/s2.求:
(1)动摩擦因数μ的大小;
(2)t=0.4s时滑块的速度v的大小.
分析 (1)根据图象得出0.1s时的加速度大小,结合牛顿第二定律求出动摩擦因数的大小.
(2)根据0.2s时的速度,结合速度时间公式求出速度减为零的时间,然后求出匀加速下滑的加速度,结合速度时间公式求出0.4s时的速度.
解答 解:(1)由图象可知0.1s物体离开弹簧向上做匀减速运动,
加速度的大小$a=\frac{2-1}{0.2-0.1}m/{s}^{2}=10m/{s}^{2}$,
根据牛顿第二定律,有:$a=\frac{mgsin37°+μmgcos37°}{m}$=gsin37°+μgcos37°=10m/s2,
解得:μ=0.5.
(2)根据速度时间公式,得:t1=0.3s时的速度大小v1=v0-t=1-10×0.1m/s=0m/s.
返回的加速度大小a′=gsin37°-μgcos37°=6-4m/s2=2m/s2,
则0.4s时的速度v2=a′t′=2×0.1m/s=0.2m/s.
答:(1)动摩擦因数μ的大小为0.5.
(2)t=0.4s时滑块的速度v的大小为0.2m/s.
点评 本题考查了牛顿第二定律和速度时间图线的综合运用,通过图线斜率求出加速度是解决本题的关键,知道加速度是联系力学和运动学的桥梁,注意上滑的加速度大小和下滑的加速度大小不等.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
4.下列关于物理学中的思想和方法叙述不正确的是( )
| A. | 一个物体受到几个力共同作用产生的效果与某一个力产生的效果相同,这个力叫做那几个力的合力,这里包含了“等效替代”的思想 | |
| B. | 在“探究弹性势能的表达式”时,为计算弹簧弹力所做的功,把拉伸弹簧的过程分为许多小段,把每一小段的弹力认为是恒力,用每小段做功的代数和代表弹力在整个过程中所做的功,这种方法叫“微元法” | |
| C. | 在探究加速度与力、质量的关系时,先保持质量不变探究加速度与力的关系,再保持力不变探究加速度与质量的关系,这种方法叫“控制变量法” | |
| D. | 根据速度定义式v=$\frac{△x}{△t}$,当△t极短时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,这种方法叫“微元法” |
8. 如图所示的正四面体四个顶点固定有电荷量为q的点电荷,其中A、C两点为正电荷,B、D两点为负电荷,a、b、C三点分别是AB边、AC边、AD边的中点,则下列关于a、b、c三点电势和电场强度的判断中正确的是( )
如图所示的正四面体四个顶点固定有电荷量为q的点电荷,其中A、C两点为正电荷,B、D两点为负电荷,a、b、C三点分别是AB边、AC边、AD边的中点,则下列关于a、b、c三点电势和电场强度的判断中正确的是( )
 如图所示的正四面体四个顶点固定有电荷量为q的点电荷,其中A、C两点为正电荷,B、D两点为负电荷,a、b、C三点分别是AB边、AC边、AD边的中点,则下列关于a、b、c三点电势和电场强度的判断中正确的是( )
如图所示的正四面体四个顶点固定有电荷量为q的点电荷,其中A、C两点为正电荷,B、D两点为负电荷,a、b、C三点分别是AB边、AC边、AD边的中点,则下列关于a、b、c三点电势和电场强度的判断中正确的是( )| A. | a、b两点的电势相等 | B. | a、c两点的电势相等 | ||
| C. | a、c两点的场强相同 | D. | a、b两点的场强相同 |
18.下列说法正确的是( )
| A. | 英国科学家伽利略在研究物体变速运动规律时,做了著名的“斜面实验” | |
| B. | 法拉第对电磁感应现象的研究作出了突出的贡献,他首先总结出了判断感应电流方向的规律 | |
| C. | 牛顿对物理学作出了划时代的贡献,是动力学的奠基人,所以在力学单位制中,力的单位牛顿是基本单位 | |
| D. | 元电荷e的数值最早是由物理学家密立根测得的 |
5. 如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在水平力F的作用下,A、B保持静止不动,增大F,A、B仍保持静止不动,则增大F的过程中( )
如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在水平力F的作用下,A、B保持静止不动,增大F,A、B仍保持静止不动,则增大F的过程中( )
 如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在水平力F的作用下,A、B保持静止不动,增大F,A、B仍保持静止不动,则增大F的过程中( )
如图所示,A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在水平力F的作用下,A、B保持静止不动,增大F,A、B仍保持静止不动,则增大F的过程中( )| A. | 墙对B的摩擦力增大 | B. | B对A的摩擦力增大 | ||
| C. | A对B的作用力不变 | D. | A对B的作用力增大 |
3. 甲、乙两辆汽车在不同出发点沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动情况描述正确的是( )
甲、乙两辆汽车在不同出发点沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动情况描述正确的是( )
 甲、乙两辆汽车在不同出发点沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动情况描述正确的是( )
甲、乙两辆汽车在不同出发点沿同一平直路面行驶,其v-t图象如图所示,下列对汽车运动情况描述正确的是( )| A. | 在0~20s内,甲车的速度方向改变一次 | |
| B. | 在0~20s内,乙车比甲车多走了100m | |
| C. | 在第20s末,甲、乙两车可能相遇 | |
| D. | 甲车在0~10s的加速度与10~20s的加速度相同 |
 某一小型电风扇额定电压为4.0V,额定功率为2.4W.某实验小组想通过实验描绘出小电风扇的伏安特性曲线.实验中除导线和开关外,还有以下器材可供选择:
某一小型电风扇额定电压为4.0V,额定功率为2.4W.某实验小组想通过实验描绘出小电风扇的伏安特性曲线.实验中除导线和开关外,还有以下器材可供选择: ).
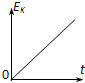
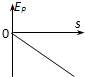
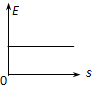
). 如图,质量为m的滑块从倾角为30°的固定斜面上无初速地释放后匀加速下滑,加速度a=$\frac{g}{4}$,取出发位置水平面为参考平面,能正确描述滑块的速率v、动能Ek、势能Ep、机械能E、时间t、位移s关系的是( )
如图,质量为m的滑块从倾角为30°的固定斜面上无初速地释放后匀加速下滑,加速度a=$\frac{g}{4}$,取出发位置水平面为参考平面,能正确描述滑块的速率v、动能Ek、势能Ep、机械能E、时间t、位移s关系的是( )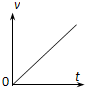
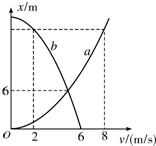 甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止.取出发点位置x=0,甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.
甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动.质点甲做初速度为零,加速度大小为a1的匀加速直线运动.质点乙做初速度为v0,加速度大小为a2的匀减速直线运动至速度减为零保持静止.取出发点位置x=0,甲、乙两质点在运动过程中的位置x-速度v图象如图所示,虚线与对应的坐标轴垂直.