题目内容
7.交叉路口处有一辆静止的小汽车等候信号灯,当绿灯亮时,它以2m/s2的加速度起动,与此同时,一辆大卡车以12m/s的速度从小汽车旁边驶过.此后小汽车保持加速度不变做匀加速直线运动但最大速度只能达到16m/s,大卡车仍以原来速度直线行驶.问:(1)小汽车追上大卡车以前,两车之间的最大距离是多少?
(2)小汽车追上大卡车时距起动位置多远?
分析 (1)当两车速度相等时,相距最远,结合速度时间公式求出速度相等经历的时间,结合位移公式求出两车之间的最大距离.
(2)抓住位移关系,结合运动学公式求出追及的时间,从而结合位移公式求出小汽车追上大卡车时距离起动位置的距离.
解答 解:(1)设经过t时间速度相等,此时距离最远,
有:at1=v1,解得${t}_{1}=\frac{{v}_{1}}{a}=\frac{12}{2}s=6s$
此时小汽车的位移${x}_{1}=\frac{1}{2}a{{t}_{1}}^{2}=\frac{1}{2}×2×36m=36m$,大卡车的位移x2=v1t1=12×6m=72m,
则最大距离△x=x2-x1=72-36m=36m.
(2)设小汽车速度最大时用时t′,
a t′=16m/s,
解得t′=8s.
此时小汽车的位移x1′=$\frac{1}{2}at{′}^{2}=\frac{1}{2}×2×64m$=64m
大卡车的位移x2′=v1t′=12×8=96m,没追上,应在小汽车匀速时追上
设追上时用时t.
则有:${v}_{1}t=\frac{{{v}_{m}}^{2}}{2a}+{v}_{m}(t-\frac{{v}_{m}}{a})$,即$12t=\frac{1{6}^{2}}{4}+16×(t-\frac{16}{2})$,
解得t=16s.
小汽车追上大卡车时距起动位置 x=v1t=12×16=192m.
答:(1)小汽车追上大卡车以前,两车之间的最大距离是36m;
(2)小汽车追上大卡车时距起动位置192m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,有最远距离.

练习册系列答案
相关题目
17.由热力学第一定律知,下述说法正确的是( )
| A. | 物体若与外界绝热,就不能改变其内能 | |
| B. | 外界对物体做正功时,物体的内能一定增加 | |
| C. | 外界对物体做负功、物体又放热时,其内能一定减少 | |
| D. | 外界对物体做正功、物体又放热时,其内能可能增加 |
18.如图所示是在高速公路是哪个用测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到信号间的时间差测出被测物体的速度.图中P1、P2是测速仪发出的超声波信号,n1、n2分别是P1、P2由汽车反射回来的信号,设测速仪匀速扫描,P1、P2之间的时间间隔△t=1.0s,超声波在空气中的传播速度是v=340m/s,若汽车的运动情况是( )(汽车运动方向沿车与测速仪的连线)


| A. | 汽车在靠近超声波测速仪,速度大小为17.0m/s | |
| B. | 汽车在靠近超声波测速仪,速度大小为17.9m/s | |
| C. | 汽车在远离超声波测速仪,速度大小为17.0m/s | |
| D. | 汽车在远离超声波测速仪,速度大小为17.9m/s |
15.汽车以36km/h的速度行驶,突然遇到紧急情况开始刹车,加速度的大小为4m/s2,从刹车开始,经过5s,汽车通过的位移为( )
| A. | 0 | B. | 10m | C. | 12.5m | D. | 37.5m |
2.汽车从静止开始作匀变速直线运动,第4秒末关闭发动机,再经6秒停止,汽车一共行驶了40米则( )
| A. | 在运动过程中的最大速度为8m/s | |
| B. | 在运动过程中的最大速度为5m/s | |
| C. | 加速阶段的加速度的大小为2m/s2 | |
| D. | 减速阶段的加速度的大小为1.5m/s2 |
12.下列说法正确的是( )
| A. | “北京时间10点整”,指的是时间 | |
| B. | 列车在上海站停了8min,指的是时间 | |
| C. | 一节课是40min,指的是时刻 | |
| D. | “今天晚上7:30,你一定在家等我吗?”,这里指的是时间 |
8.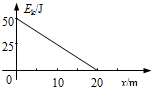 在未知方向的力F作用下,一质量为1.0kg的物体以一定的初速度在光滑水平面上作直线运动.物体的动能Ek随位移x变化的关系如图所示.(g=10m/s2)由上述已知条件,可求出( )
在未知方向的力F作用下,一质量为1.0kg的物体以一定的初速度在光滑水平面上作直线运动.物体的动能Ek随位移x变化的关系如图所示.(g=10m/s2)由上述已知条件,可求出( )
 在未知方向的力F作用下,一质量为1.0kg的物体以一定的初速度在光滑水平面上作直线运动.物体的动能Ek随位移x变化的关系如图所示.(g=10m/s2)由上述已知条件,可求出( )
在未知方向的力F作用下,一质量为1.0kg的物体以一定的初速度在光滑水平面上作直线运动.物体的动能Ek随位移x变化的关系如图所示.(g=10m/s2)由上述已知条件,可求出( )| A. | 力F的最小值为2.5N | |
| B. | 力F不可能大于10N | |
| C. | 物体运动过程中在任意位置的加速度大小 | |
| D. | 物体运动过程中在任意位置力F的功率 |