题目内容
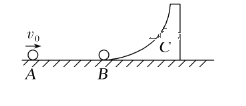
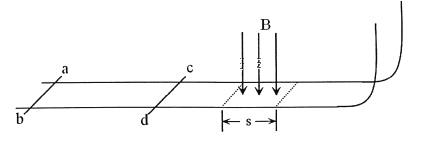
【题目】如图所示，有两根足够长的平行光滑导轨水平放置，右侧用一小段光滑圆弧和另一对竖直光滑导轨平滑连接，导轨间距L＝1m。细金属棒ab和cd垂直于导轨静止放置，它们的质量m均为1kg，电阻R均为0.5Ω。cd棒右侧lm处有一垂直于导轨平面向下的矩形匀强磁场区域，磁感应强度B＝1T，磁场区域长为s。以cd棒的初始位置为原点，向右为正方向建立坐标系。现用向右的水平恒力F＝1.5N作用于ab棒上，作用4s后撤去F。撤去F之后ab棒与cd棒发生弹性碰撞，cd棒向右运动。金属棒与导轨始终接触良好，导轨电阻不计，空气阻力不计。（g=10m/s2）求：
(1) ab棒与cd棒碰撞后瞬间的速度分别为多少；
(2)若s＝1m，求cd棒滑上右侧竖直导轨，距离水平导轨的最大高度h；
(3)若可以通过调节磁场右边界的位置来改变s的大小，写出cd棒最后静止时与磁场左边界的距离x的关系。（不用写计算过程）
【答案】（1）0，
；（2）1.25 m；（3）见解析
【解析】
(1)对ab棒，由动量定理得
ab棒与cd棒碰撞过程，取向右方向为正，对系统由动量守恒定律得
由系统机械能守恒定律得
解得
，
(2)由安培力公式可得
对cd棒进入磁场过程，由动量定理得
设导体棒cd进出磁场时回路磁通量变化量为
以上几式联立可得
。
对cd棒出磁场后由机械能守恒定律可得
联立以上各式得
。
(3)第一种情况如果磁场s足够大，cd棒在磁场中运动距离
时速度减为零，由动量定理可得
设磁通量变化量为
流过回路的电量
联立可得
即s≥6 m，x=6 m，停在磁场左边界右侧6m处。
第二种情况cd棒回到磁场左边界仍有速度，这时会与ab再次发生弹性碰撞，由前面计算可得二者速度交换，cd会停在距磁场左边界左侧1m处，设此种情况下磁场区域宽度
，向右运动时有
返回向左运动时
通过回路的电量
联立可得
即s＜3 m时，x=1 m，停在磁场左边界左侧1m处；
第三种情况3 m≤s＜6 m，
向右运动时有
通过回路的电量
返回向左运动时
通过回路的电量
联立可得x=(2s－6）m，在磁场左边界右侧。
