题目内容
8. 如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球通过管的最高点,且小球在最高点时对管壁有向下的压力,求v0必须满足的条件.
如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球通过管的最高点,且小球在最高点时对管壁有向下的压力,求v0必须满足的条件.
分析 若小球在最高点时对管壁有向下的压力,则管壁对小球有向上的支持力,则小球所受重力和支持力的合力提供向心力,小球的速度再根据从最低点到最高点的过程中,只有重力做功,由机械能守恒即可求解范围.
解答 解:在最高点小球的重力和管壁对小球的支持力提供向心力,则有:
mg-T=$\frac{{v}^{2}}{R}$,
当T=0时,速度最大,解得:
v=$\sqrt{gR}$
所以当0≤v<$\sqrt{gR}$时,小球在最高点时对管壁有向下的压力,从最低点到最高点的过程中,只有重力做功,由机械能守恒得:
$\frac{1}{2}$mv02=mg•2R+$\frac{1}{2}$mv2
当v=0时,解得:${v}_{0}=2\sqrt{gR}$,
当v=$\sqrt{gR}$时,解得:${v}_{0}=\sqrt{5gR}$
所以v0的范围为:$2\sqrt{gR}$≤v0<$\sqrt{5gR}$
答:v0必须满足的条件为$2\sqrt{gR}$≤v0<$\sqrt{5gR}$.
点评 本题主要考查了机械能守恒定律、圆周运动向心力公式的直接应用,知道双轨道模型,轨道对小球既能提供支持力,又能提供拉力,难度适中.

练习册系列答案
相关题目
2. 在互成角度的两个力的合成的实验中,橡皮条的一端固定在A点,另一端被两个弹簧秤拉到O点,两弹簧秤读数分别为F1和F2,细绳方向分别与OA直线延长线的夹角为α1和α2,如图所示,以下说法正确的是( )
在互成角度的两个力的合成的实验中,橡皮条的一端固定在A点,另一端被两个弹簧秤拉到O点,两弹簧秤读数分别为F1和F2,细绳方向分别与OA直线延长线的夹角为α1和α2,如图所示,以下说法正确的是( )
 在互成角度的两个力的合成的实验中,橡皮条的一端固定在A点,另一端被两个弹簧秤拉到O点,两弹簧秤读数分别为F1和F2,细绳方向分别与OA直线延长线的夹角为α1和α2,如图所示,以下说法正确的是( )
在互成角度的两个力的合成的实验中,橡皮条的一端固定在A点,另一端被两个弹簧秤拉到O点,两弹簧秤读数分别为F1和F2,细绳方向分别与OA直线延长线的夹角为α1和α2,如图所示,以下说法正确的是( )| A. | 若O点的位置不变,则合力不变 | |
| B. | 用平行四边形定则求得的合力F一定沿OA直线方向OO′ | |
| C. | 若不改变O和α1,F1增大,F2必减小 | |
| D. | 合力F必大于F1或F2 |
3. 如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球由竖直平面内的A点匀速率运动到B点.下列有关瞬时功率的说法正确的是( )
如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球由竖直平面内的A点匀速率运动到B点.下列有关瞬时功率的说法正确的是( )
 如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球由竖直平面内的A点匀速率运动到B点.下列有关瞬时功率的说法正确的是( )
如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球由竖直平面内的A点匀速率运动到B点.下列有关瞬时功率的说法正确的是( )| A. | 重力的功率逐渐减小 | B. | 重力的功率逐渐增大 | ||
| C. | 拉力的功率逐渐减小 | D. | 拉力的功率逐渐增大 |
20. 如图所示,球网高出球台H,网到球台边的距离为L,某人在乒乓球训练中,从左侧$\frac{L}{2}$处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧台面边缘,设乒乓球运动为平抛运动,忽略一切阻力,则( )
如图所示,球网高出球台H,网到球台边的距离为L,某人在乒乓球训练中,从左侧$\frac{L}{2}$处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧台面边缘,设乒乓球运动为平抛运动,忽略一切阻力,则( )
 如图所示,球网高出球台H,网到球台边的距离为L,某人在乒乓球训练中,从左侧$\frac{L}{2}$处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧台面边缘,设乒乓球运动为平抛运动,忽略一切阻力,则( )
如图所示,球网高出球台H,网到球台边的距离为L,某人在乒乓球训练中,从左侧$\frac{L}{2}$处,将球沿垂直于网的方向水平击出,球恰好通过网的上沿落到右侧台面边缘,设乒乓球运动为平抛运动,忽略一切阻力,则( )| A. | 击球点的高度与网高度之比为2:1 | |
| B. | 乒乓球在网左右两侧运动时间之比为2:1 | |
| C. | 乒乓球过网时与落到台面边缘时竖直方向速率之比为1:2 | |
| D. | 乒乓球在左、右两侧运动速度变化量之比为1:2 |
17.下列说法正确的是( )
| A. | 凡是大小相等、方向相反、分别作用在两个物体上的两个力必定是一对作用力和反作用力 | |
| B. | 凡是大小相等、方向相反、作用在同一物体上的两个力必定是一对作用力和反作用力 | |
| C. | 即使大小相等、方向相反、作用在同一直线上且分别作用在两个物体上的两个力也不一定是一对作用力和反作用力 | |
| D. | 相互作用的一对力究竟称哪一个力是反作用力不是任意的 |
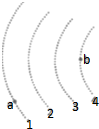 如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26ev和5ev.当这一点电荷运动到等势面3位置时的动能为12ev,当该电荷运动到某一位置,其电势能变为-8ev时,它们动能应为20ev.
如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26ev和5ev.当这一点电荷运动到等势面3位置时的动能为12ev,当该电荷运动到某一位置,其电势能变为-8ev时,它们动能应为20ev. 如图所示,一光滑且足够长的斜面固定在地面上,斜面倾角θ=30°,平行于斜面的轻弹簧劲度系数为k=800N/m,一端固定在斜面底端,另一端与物块A拴接,物块B沿斜面叠放在物块A上但不粘连.物块A质量mA=1.5kg、物块B质量mB=10.5kg,初始t0=0时刻两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做匀加速运动.已知力F在t=0.2s内是变力,在0.2s后是恒力;弹簧始终在弹性限度内,且弹簧形变量等大时弹性势能也等大,g取10m/s2.求:
如图所示,一光滑且足够长的斜面固定在地面上,斜面倾角θ=30°,平行于斜面的轻弹簧劲度系数为k=800N/m,一端固定在斜面底端,另一端与物块A拴接,物块B沿斜面叠放在物块A上但不粘连.物块A质量mA=1.5kg、物块B质量mB=10.5kg,初始t0=0时刻两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做匀加速运动.已知力F在t=0.2s内是变力,在0.2s后是恒力;弹簧始终在弹性限度内,且弹簧形变量等大时弹性势能也等大,g取10m/s2.求: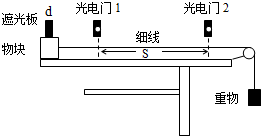 如图所示为测量物块与水平固定桌面之间动摩擦因数的实验装置示意图,细线平行于桌面,已知物块和遮光板的总质量为M,重物质量为m,遮光板的宽度为d,两光电门之间的距离为s,重力加速度为g,让物块从光电门1的左侧由静止释放,分别测出遮光板通过光电门1、2所用的时间t1、t2,用遮光板通过光电门的平均速度表示遮光板竖直中线通过光电门的瞬时速度.
如图所示为测量物块与水平固定桌面之间动摩擦因数的实验装置示意图,细线平行于桌面,已知物块和遮光板的总质量为M,重物质量为m,遮光板的宽度为d,两光电门之间的距离为s,重力加速度为g,让物块从光电门1的左侧由静止释放,分别测出遮光板通过光电门1、2所用的时间t1、t2,用遮光板通过光电门的平均速度表示遮光板竖直中线通过光电门的瞬时速度. 如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则:
如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则: