题目内容
7. 如图所示,地面上有一固定的球面,球半径为R,球面的斜上方P处有一质点(P与球心O在同一竖直平面内).已知P到球心O的距离为L,P到地面的垂直距离为H,现要使此质点从静止开始沿一光滑斜直轨道在最短时间内滑到球面上,求所需的最短时间.
如图所示,地面上有一固定的球面,球半径为R,球面的斜上方P处有一质点(P与球心O在同一竖直平面内).已知P到球心O的距离为L,P到地面的垂直距离为H,现要使此质点从静止开始沿一光滑斜直轨道在最短时间内滑到球面上,求所需的最短时间.
分析 先求证小球从竖直平面的圆顶点沿光滑轨道运动到任何方向圆外边缘的时间相同,且求出关系式;作图找出最短时间的运动轨道,根据三角关系求出相关的物理量,求出最短时间.
解答 解:(1)求证:如图所示小球从竖直平面的半径为R′的圆的顶点,沿光滑轨道运动到任何方向圆外边缘,
任取一条轨道PQ,PQ与水平面的夹角为Φ,
由三角关系得PQ的长度为:l=2R′sinΦ
由牛顿第二定律得,沿光滑斜面下滑的加速度为:a=gsinΦ
由位移时间公式得,运动时间:t=$\sqrt{\frac{2l}{a}}=\sqrt{\frac{2×2R′sinΦ}{gsinΦ}}=2\sqrt{\frac{R′}{g}}$
即运动时间与角度无关,故对应任何轨道的时间均相同.
(2)作图:以P为顶点作一半径为r的球面,使其与所给球面相切与Q,如图所示:
由(1)可知右上圆内从P点到圆的外边缘的时间是相同的,故PQ1、PQ2用时均长于PQ用时,
则线段PQ即为所求的用时最短的轨道.
(3)解题:把上图转化如下: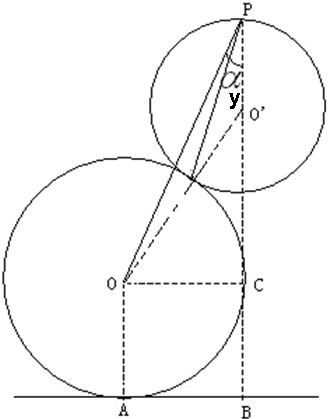
∠OPO′=α,
由三角关系得:cosα=$\frac{\overline{PC}}{\overline{OP}}=\frac{H-R}{L}$
(R+r)2=L2+r2-2Lrcosα
联立以上两式解得:$r=\frac{{L}^{2}-{R}^{2}}{2H}$
由(1)知,运动时间:${t}_{min}=2\sqrt{\frac{r}{g}}=2\sqrt{\frac{\frac{{L}^{2}-{R}^{2}}{2H}}{g}}=\sqrt{\frac{2({L}^{2}-{R}^{2})}{Hg}}$
答:所需的最短时间为$\sqrt{\frac{2({L}^{2}-{R}^{2})}{Hg}}$.
点评 本题很难,需要综合运用数学知识和物理知识,对于作图要求较高,需要准确掌握三角形相关的数学知识.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案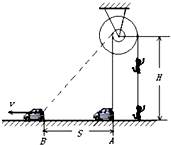 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.为此导演在某房顶离地H=8m处架设了轮轴,如图所示,轮和轴的直径之比为3:1,特技演员的质量m=60kg,若轨道车从图中A前进s=6m到B处时速度为v=5m/s,人和车可视为质点,轮轴的质量不计,轮轴的大小相对于H可忽略,g取10m/s2.则这一过程中( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.为此导演在某房顶离地H=8m处架设了轮轴,如图所示,轮和轴的直径之比为3:1,特技演员的质量m=60kg,若轨道车从图中A前进s=6m到B处时速度为v=5m/s,人和车可视为质点,轮轴的质量不计,轮轴的大小相对于H可忽略,g取10m/s2.则这一过程中( )| A. | 演员上升的高度h=5m | B. | 演员上升的高度h=6m | ||
| C. | 演员重力对其做的功W=3600J | D. | 演员的速度变化量是9m/s |
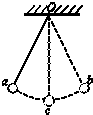 如图所示,将一个小球用细线悬挂起来,让小球在a、b之间来回摆动,c点为小球圆弧轨迹的最低点,则以下说法中正确的是( )
如图所示,将一个小球用细线悬挂起来,让小球在a、b之间来回摆动,c点为小球圆弧轨迹的最低点,则以下说法中正确的是( )| A. | 小球做简谐振动的回复力是摆球重力沿圆弧线方向的分力 | |
| B. | 小球由c到b的过程,动能减小,重力势能增大 | |
| C. | 小球在c点时的重力势能最大,向心加速度也最大 | |
| D. | 在平衡位置时,摆线张力最大,回复力也最大 |
| A. | 不同的物体,若温度相同,则内能也相同 | |
| B. | 物体速度增大,则分子动能增大,内能也增大 | |
| C. | 冰熔化时,吸收热量,温度不变,但内能增大 | |
| D. | 静止在地面上的物体,机械能和内能均为零 |
| A. | 直接对准目标 | B. | 向西偏一些 | C. | 向东偏一些 | D. | 无法确定 |

 如图所示,长为l的木板A静止于水平地面上,一物体B以速度v0冲上A,A、B分别做匀加速和匀减速运动,加速度大小分别为aA和aB,若使B刚好不滑离A,v0应为多大?
如图所示,长为l的木板A静止于水平地面上,一物体B以速度v0冲上A,A、B分别做匀加速和匀减速运动,加速度大小分别为aA和aB,若使B刚好不滑离A,v0应为多大?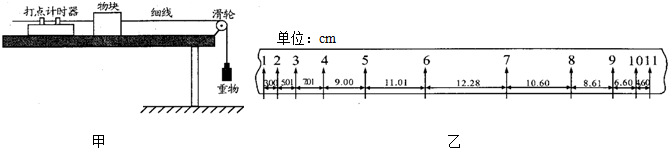
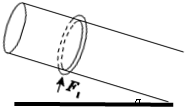 如图,倾斜的长直杆与水平面成α角,一个质量为m的圆环套在一根固定的长直杆上,直杆截面为圆形,直径略小于圆环直径,环与杆的动摩擦因数为μ.现给环一个沿杆方向向下的恒力F,使圆环由静止开始运动,同时对环施加一个竖直向上、大小随速度变化的作用力F1=kv,其中k为常数,分析圆环的运动,求:
如图,倾斜的长直杆与水平面成α角,一个质量为m的圆环套在一根固定的长直杆上,直杆截面为圆形,直径略小于圆环直径,环与杆的动摩擦因数为μ.现给环一个沿杆方向向下的恒力F,使圆环由静止开始运动,同时对环施加一个竖直向上、大小随速度变化的作用力F1=kv,其中k为常数,分析圆环的运动,求: