Question

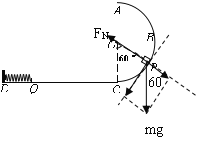
【题目】如图，半径为R的光滑半圆形轨道ABC在竖直平面内，与水平轨道CD相切于C 点， D端有一被锁定的轻质压缩弹簧，弹簧左端连接在固定的挡板上，弹簧右端Q到C点的距离为2R。质量为m可视为质点的滑块从轨道上的P点由静止滑下，刚好能运动到Q点，且恰能触发弹簧解除锁定，然后滑块被弹回，且刚好能通过圆轨道的最高点A。已知∠POC=60°，求：

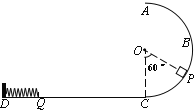
（1）滑块第一次滑至圆形轨道最低点C时对轨道压力；

（2）弹簧被锁定时具有的弹性势能；

（3）小球返回到P点时的加速度大小。

Answer 1

【答案】（1） （2） （3）

【解析】（1）设滑块第一次滑至C点时的速度为vc，圆轨道C点对滑块的支持力为FN

P→C过程： mgR(1-cos60°) =mv2

C点：FN-mg=m

解得FN=2mg

由牛顿第三定律得：滑块对轨道C点的压力大小FN′=2mg，方向竖直向下

（2）对P→C→Q过程：mgR(1-cos60°)-μmg2R=0

解得μ=0.25

A点：mg=m

Q→C→A过程：Ep=mvA2+mg2R+μmg2R

解得：Ep=3mgR

（3）P→A过程由动能定理

在P点受力分析如图