题目内容
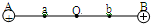 在光滑的绝缘水平面上,相隔2L的A、B两点固定有两个电量均为Q的正点电荷,a、O、b是A、B连线上的三点,O为中点,Oa=Ob=
在光滑的绝缘水平面上,相隔2L的A、B两点固定有两个电量均为Q的正点电荷,a、O、b是A、B连线上的三点,O为中点,Oa=Ob=| L | 2 |
(1)a点的场强大小;(2)恒定阻力的大小;(3)a点的电势.
分析:(1)根据场强的叠加,通过点电荷的场强公式求出a点处的场强.
(2)电荷最终停止在o点,该过程中只有阻力做功,根据动能定理求出阻力的大小.
(3)根据动能定理求出a→o过程电场力做功,从而得出ao间的电势差,抓住o点的电势为0,求出a点的电势.
(2)电荷最终停止在o点,该过程中只有阻力做功,根据动能定理求出阻力的大小.
(3)根据动能定理求出a→o过程电场力做功,从而得出ao间的电势差,抓住o点的电势为0,求出a点的电势.
解答:解:(1)a点处的场强:Ea=k
-k
=
(2)根据等量同种电荷的电场特点可知,关于O对称的ab两点的电势是相等的,所以从a到b,由0-
mv02=-f?L,可求得:f=
(3)从a到O电场力与阻力做功,n
mv02-
mv02=(φa-0)q-f?
L,
所以:φa=
( nmv02-mv02+fL)=
(n-
) mv02
答:(1)a点的场强大小
;(2)恒定阻力的大小
;(3)a点的电势为
(n-
) mv02
| Q | ||
(
|
| Q | ||
(
|
| 32KQ |
| 9L2 |
(2)根据等量同种电荷的电场特点可知,关于O对称的ab两点的电势是相等的,所以从a到b,由0-
| 1 |
| 2 |
| mv02 |
| 2L |
(3)从a到O电场力与阻力做功,n
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以:φa=
| 1 |
| 2q |
| 1 |
| 2q |
| 1 |
| 2 |
答:(1)a点的场强大小
| 32KQ |
| 9L2 |
| mv02 |
| 2L |
| 1 |
| 2q |
| 1 |
| 2 |
点评:本题考查了场强的叠加,以及动能定理的运用,综合性较强,对学生的能力要求较高,需加强训练.

练习册系列答案
相关题目
 (2011?广元模拟)在光滑的绝缘水平面上,A、A两球(均可看成质点)位于X轴上,A球带电,B球不带电.开始时B球静置于场强为E=1×103N/C的水平勻强电场的边缘(如图所示),A球从原点开始经过2s后与B球碰撞,碰后合为一体在电场中运动,A、B系统的动能与坐标的部分关系如图所示,则:
(2011?广元模拟)在光滑的绝缘水平面上,A、A两球(均可看成质点)位于X轴上,A球带电,B球不带电.开始时B球静置于场强为E=1×103N/C的水平勻强电场的边缘(如图所示),A球从原点开始经过2s后与B球碰撞,碰后合为一体在电场中运动,A、B系统的动能与坐标的部分关系如图所示,则: 如图所示,在光滑的绝缘水平面上,一个宽度a=10cm、长度b=15cm、电阻为1Ω、质量为0.1kg的闭合金属框以v0=10m/s的初速度向一有界匀强磁场滑去,磁场的磁感应强度为0.5T.
如图所示,在光滑的绝缘水平面上,一个宽度a=10cm、长度b=15cm、电阻为1Ω、质量为0.1kg的闭合金属框以v0=10m/s的初速度向一有界匀强磁场滑去,磁场的磁感应强度为0.5T. (2011?山西二模)如图所示,两个带等量正电荷的小球A、B(可视为点电荷),被固定在光滑的绝缘水平面上.P、N是小球连线的中垂线上的两点,且PO=ON.现将一个电荷量很小的带负电的小球C(可视为质点),由P点静止释放,在小球C向N点运动的过程中,下列关于小球C的速度、加速度的图象中,可能正确的是( )
(2011?山西二模)如图所示,两个带等量正电荷的小球A、B(可视为点电荷),被固定在光滑的绝缘水平面上.P、N是小球连线的中垂线上的两点,且PO=ON.现将一个电荷量很小的带负电的小球C(可视为质点),由P点静止释放,在小球C向N点运动的过程中,下列关于小球C的速度、加速度的图象中,可能正确的是( ) 如图所示,质量均为m的三个带电小球,A、B、C放置在光滑的绝缘水平面上,A与B、B与C相距均为l,A带电QA=+8q,B带电QB=+q,若在C 上加一水平向右的恒力F,能使A、B、C三球始终保持相对静止,则:
如图所示,质量均为m的三个带电小球,A、B、C放置在光滑的绝缘水平面上,A与B、B与C相距均为l,A带电QA=+8q,B带电QB=+q,若在C 上加一水平向右的恒力F,能使A、B、C三球始终保持相对静止,则: