题目内容
 如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:
如图所示,一个半径为R的光滑圆弧轨道APB竖直固定放置,PQ为其竖直对称轴,∠AOQ与∠BOQ都等于θ.现让一可看做质点的小球在轨道内侧运动,当其冲出A点后恰好可以从B点再进入轨道,所以此运动可以周而复始进行.已知小球质量为m,重力加速度为g,试求:(1)小球离开轨道后的最高点距直线AB的距离;
(2)若要小球在最低点时对轨道的压力最小,θ应为多少?对应的最小压力为多少?
分析:(1)将速度进行分解,在水平方向上做匀速直线运动,在竖直方向上做竖直上抛运动,根据运动学规律,结合几何关系求出小球离开轨道后上升到最高点距直线AB的距离.
(2)根据动能定理和牛顿第二定律求出物体在最低点所受的支持力的大小,根据数学求极值的方法求出最小值.
(2)根据动能定理和牛顿第二定律求出物体在最低点所受的支持力的大小,根据数学求极值的方法求出最小值.
解答:解:(1)物体刚冲出A点时,将物体的速度分解有: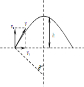
v1=vcosθ… ①
v2=vsinθ…②
在抛出到最高点过程中,水平方向上为匀速直线运动,有:Rsinθ=v1t…③
竖直方向上为匀变速直线运动,末速度为零,逆过来看是自由落体运动.有
v2=gt…④
h=
gt2…⑤
由①②③④解得v=
… ⑥
t=sinθ
… ⑦
由⑤得,h=
… ⑧
(2)设物体在最低点的速度为v′,则物体从A到运动到最低点的过程中,由动能定理得,
mgR(1-cosθ)=
m(v′2-v2)… ⑨
在最低点由向心力公式得,
N-mg=m
… ⑩
由⑥⑨⑩得,N=mg(3+2cosθ+
)
分析知当θ=45°时,N最小,为N=(3+2
)mg.
答:(1)小球离开轨道后的最高点距直线AB的距离为
.
(2)当θ=45°时,压力最小,为N=(3+2
)mg.

v1=vcosθ… ①
v2=vsinθ…②
在抛出到最高点过程中,水平方向上为匀速直线运动,有:Rsinθ=v1t…③
竖直方向上为匀变速直线运动,末速度为零,逆过来看是自由落体运动.有
v2=gt…④
h=
| 1 |
| 2 |
由①②③④解得v=
|
t=sinθ
|
由⑤得,h=
| Rsin2θ |
| 2cosθ |
(2)设物体在最低点的速度为v′,则物体从A到运动到最低点的过程中,由动能定理得,
mgR(1-cosθ)=
| 1 |
| 2 |
在最低点由向心力公式得,
N-mg=m
| v′2 |
| R |
由⑥⑨⑩得,N=mg(3+2cosθ+
| 1 |
| cosθ |
分析知当θ=45°时,N最小,为N=(3+2
| 2 |
答:(1)小球离开轨道后的最高点距直线AB的距离为
| Rsin2θ |
| 2cosθ |
(2)当θ=45°时,压力最小,为N=(3+2
| 2 |
点评:本题综合考查了动能定理、牛顿第二定律等知识,综合性较强,对学生的能力要求较高,需加强该类题型的训练.

练习册系列答案
相关题目
 如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则绳子的拉力T和墙壁的弹力N分别是( )
如图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则绳子的拉力T和墙壁的弹力N分别是( ) (2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°.
(2005?浦东新区一模)如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°. (2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上
(2012?山西二模)如图所示,一个半径为R、质量为M的半圆形光滑小碗,在它的边上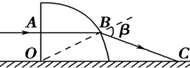 如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则:
如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点.已知OA=,该圆柱体对蓝光的折射率为,则: