题目内容
8.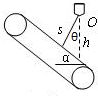 如图所示为某制药厂自动生产流水线上的一部分装置示意图,已知传送带与水平面的夹角为α,O为漏斗,要使药品从漏斗出来经光滑槽送到传送带上,设滑槽与竖直方向的夹角为θ,则θ为多大时可使药片滑到传送带上的时间最短?
如图所示为某制药厂自动生产流水线上的一部分装置示意图,已知传送带与水平面的夹角为α,O为漏斗,要使药品从漏斗出来经光滑槽送到传送带上,设滑槽与竖直方向的夹角为θ,则θ为多大时可使药片滑到传送带上的时间最短?
分析 根据牛顿第二定律求出在斜面上运动的加速度大小,根据几何关系求出斜面的长度,再根据x=$\frac{1}{2}a{t}^{2}$得到时间的表达式,由数学知识求解.
解答 解:由正弦定理得,$\frac{s}{sin(90°-α)}$=$\frac{h}{sin[180°-θ-(90°-α)]}$
解得:s=$\frac{hcosα}{cos(θ-α)}$
加速度为 a=$\frac{mgcosθ}{m}$=gcosθ
由s=$\frac{1}{2}a{t}^{2}$得:t=$\sqrt{\frac{2s}{a}}$=$\sqrt{\frac{2hcosα}{gcos(θ-α)cosθ}}$
设y=gcos(θ-α)cosθ,则y的导数为 y′=g[-sin(θ-α)cosθ-cos(θ-α)sinθ]=gsin(α-2θ)
当y′=0时,即θ=$\frac{α}{2}$时y有最大,t有最小值.
答:θ为$\frac{α}{2}$时可使药片滑到传送带上的时间最短.
点评 解决本题的关键运用牛顿第二定律和运动学公式得到时间表达式,运用数学知识分析和求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.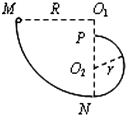 竖直放置的固定绝缘光滑轨道由半径分别为R的$\frac{1}{4}$圆弧MN和半径为r的半圆弧NP拼接而成(两段圆弧相切于N点),小球带正电,质量为m,电荷量为q.已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力.下列说法正确的是( )
竖直放置的固定绝缘光滑轨道由半径分别为R的$\frac{1}{4}$圆弧MN和半径为r的半圆弧NP拼接而成(两段圆弧相切于N点),小球带正电,质量为m,电荷量为q.已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力.下列说法正确的是( )
 竖直放置的固定绝缘光滑轨道由半径分别为R的$\frac{1}{4}$圆弧MN和半径为r的半圆弧NP拼接而成(两段圆弧相切于N点),小球带正电,质量为m,电荷量为q.已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力.下列说法正确的是( )
竖直放置的固定绝缘光滑轨道由半径分别为R的$\frac{1}{4}$圆弧MN和半径为r的半圆弧NP拼接而成(两段圆弧相切于N点),小球带正电,质量为m,电荷量为q.已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力.下列说法正确的是( )| A. | 若加竖直向上的匀强电场E(Eq<mg),则小球能通过P点 | |
| B. | 若加竖直向下的匀强电场,则小球不能通过P点 | |
| C. | 若加垂直纸面向里的匀强磁场,则小球不能通过P点 | |
| D. | 若加垂直纸面向外的匀强磁场,则小球不能通过P点 |
3.某实验小组为了描绘一只“4V 2W“的小灯泡的伏安特性曲线,除导线和开关外还准备了以下器材可供选择:
Α.电流表Α,(量程0.6A,内阻约为1Ω)
Β.电流表Α2 (量程3.OA,内阻约为0.2Ω)
C.电压表V1(量程5V,内阻约为5kΩ)
D.电压表V2(量程15.0V,内阻约为15kΩ)
E.滑动变阻器R1(最大电阻为500Ω,额定电流500mA)
F.滑动变阻器(最大电阻为10Ω,额定电流2.0Α)
G.电源(电动势为6.0V,内阻约为1.5Ω)

(1)实验中所用的电流表应选A;电压表选C;滑动变阻器应选F.(只需填器材前面的字母代号)
(2)将图甲中的实物连接成实验所需的电路(有两根导线已经接好).实验开始时,滑动变阻器的滑片应该置于最左端.(填“左”或“右”)
(3)经过正确的操作,测得的数据如表:请在图乙中描点画出小灯泡的U-I曲线.
Α.电流表Α,(量程0.6A,内阻约为1Ω)
Β.电流表Α2 (量程3.OA,内阻约为0.2Ω)
C.电压表V1(量程5V,内阻约为5kΩ)
D.电压表V2(量程15.0V,内阻约为15kΩ)
E.滑动变阻器R1(最大电阻为500Ω,额定电流500mA)
F.滑动变阻器(最大电阻为10Ω,额定电流2.0Α)
G.电源(电动势为6.0V,内阻约为1.5Ω)

(1)实验中所用的电流表应选A;电压表选C;滑动变阻器应选F.(只需填器材前面的字母代号)
(2)将图甲中的实物连接成实验所需的电路(有两根导线已经接好).实验开始时,滑动变阻器的滑片应该置于最左端.(填“左”或“右”)
(3)经过正确的操作,测得的数据如表:请在图乙中描点画出小灯泡的U-I曲线.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.1 | 2.8 | 3.2 | 3.6 | 4.0 |
| 0 | 0.12 | 0.22 | 0.30 | 0.36 | 0.40 | 0.43 | 0.46 | 0.48 | 0.49 | 0.50 |
20.一按正弦规律变化的交流电的图象如图所示,根据图象可知( )


| A. | 该交流电电压的有效值是14.1V | |
| B. | 该交流电的电压瞬时值表达式是u=20sin0.02t (V) | |
| C. | 在t=$\frac{T}{8}$(T为交流电的周期)时,该电压的大小与其有效值相等 | |
| D. | 使用这个交流电的用电器,每通过1C的电量时,电流做了14.1J的功 |
 如图所示,宽度L=1.0m的光滑金属框架MNPQ固定于水平面内,以M为坐标原点,MN方向为x轴正方向建立坐标系,x、y轴与虚线所包围的有界匀强磁场磁感应强度大小B=0.5T,方向竖直向下.现将质量m=0.1kg的金属棒ab放在框架上,与y轴重合,受到F=0.7N的力作用后,由静止沿x轴方向运动,经0.5s通过AB,接着一直做a=2m/s2的匀加速直线运动.PM段电阻为1Ω,其它部分电阻不计.求
如图所示,宽度L=1.0m的光滑金属框架MNPQ固定于水平面内,以M为坐标原点,MN方向为x轴正方向建立坐标系,x、y轴与虚线所包围的有界匀强磁场磁感应强度大小B=0.5T,方向竖直向下.现将质量m=0.1kg的金属棒ab放在框架上,与y轴重合,受到F=0.7N的力作用后,由静止沿x轴方向运动,经0.5s通过AB,接着一直做a=2m/s2的匀加速直线运动.PM段电阻为1Ω,其它部分电阻不计.求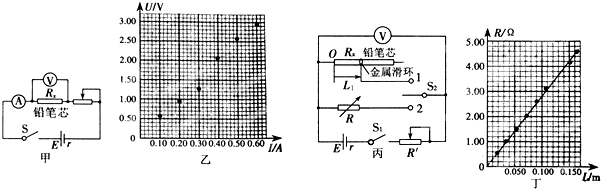
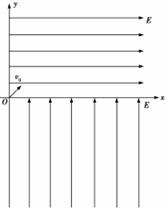 如图所示,在xOy坐标系的第一象限里有平行于坐标平面向右的匀强电场,在第四象限有平行于坐标平面向上的匀强电场,两个电场的场强大小相等,同时在第四象限还有垂直于坐标平面的匀强磁场(图中未画出),一带电小球从坐标原点O,以与x轴正向成45°向上的初速度v0射入第一象限的电场,已知小球的质量为m,带电荷量为+q,电场的场强大小E=$\frac{mg}{q}$,小球在第四象限中运动,恰好不能进入第三象限,求:
如图所示,在xOy坐标系的第一象限里有平行于坐标平面向右的匀强电场,在第四象限有平行于坐标平面向上的匀强电场,两个电场的场强大小相等,同时在第四象限还有垂直于坐标平面的匀强磁场(图中未画出),一带电小球从坐标原点O,以与x轴正向成45°向上的初速度v0射入第一象限的电场,已知小球的质量为m,带电荷量为+q,电场的场强大小E=$\frac{mg}{q}$,小球在第四象限中运动,恰好不能进入第三象限,求: