题目内容
【题目】如图甲所示，水平面上的两光滑金属导轨平行固定放置，间距d＝0.5 m，电阻不计，左端通过导线与阻值R＝2 Ω的电阻连接，右端通过导线与阻值RL＝4 Ω的小灯泡L连接。在CDFE矩形区域内有竖直向上的匀强磁场，CE长 l＝2 m，有一阻值r＝2 Ω的金属棒PQ放置在靠近磁场边界CD处(恰好不在磁场中)。CDFE区域内磁场的磁感应强度B随时间变化如图乙所示。在t＝0至t＝4 s内，金属棒PQ保持静止，在t＝4 s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动。已知从t＝0开始到金属棒运动到磁场边界EF处的整个过程中，小灯泡的亮度没有发生变化。求：
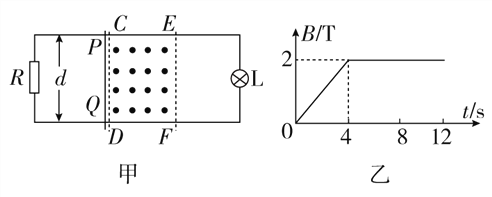
(1)通过小灯泡的电流；
(2)金属棒PQ在磁场区域中运动的速度大小。
【答案】（1）0.1A（2）1m/s
【解析】试题分析：(1) 在t＝0至t＝4 s内，金属棒PQ保持静止，磁场变化导致电路中产生感应电动势。电路为r与R并联，再与RL串联，电路的总电阻
R总＝RL＋
＝5 Ω（2分）
此时感应电动势
E＝
＝dl
＝0.5×2×0.5 V＝0.5 V（2分）
通过小灯泡的电流为：I＝
＝0.1 A。（2分）
(2) 当棒在磁场区域中运动时，由导体棒切割磁感线产生电动势，电路为R与RL并联，再与r串联，此时电路的总电阻
R总′＝r＋
＝
Ω＝
Ω（2分）
由于灯泡中电流不变，所以灯泡的电流IL＝I＝0.1 A，则流过金属棒的电流为
I′＝IL＋IR＝IL＋
＝0.3 A（2分）
电动势E′＝I′R总′＝Bdv（1分）
解得棒PQ在磁场区域中运动的速度大小
v＝1 m/s（1分）
练习册系列答案
相关题目
