题目内容
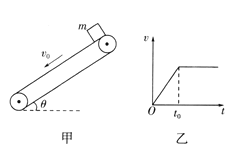
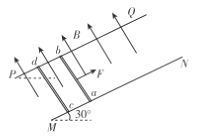
【题目】如图所示,两根足够长的粗糙平行金属导轨MN和PQ倾斜放置,其构成的平面与水平面成![]() 角,导轨间距
角,导轨间距![]() ,导轨电阻不计。两根完全相同的金属杆ab和cd分别垂直于导轨放置,且与导轨始终接触良好,整个装置处在垂直于导轨平面向上的匀强磁场中,磁场的磁感应强度
,导轨电阻不计。两根完全相同的金属杆ab和cd分别垂直于导轨放置,且与导轨始终接触良好,整个装置处在垂直于导轨平面向上的匀强磁场中,磁场的磁感应强度![]() 。开始时两杆均恰好静止在轨道上而不下滑,从
。开始时两杆均恰好静止在轨道上而不下滑,从![]() 时刻对杆ab施加一个平行于导轨平面向上的力F,杆ab从静止开始沿轨道向上做匀加速直线运动,匀加速
时刻对杆ab施加一个平行于导轨平面向上的力F,杆ab从静止开始沿轨道向上做匀加速直线运动,匀加速![]() 后金属杆cd刚要开始向上运动时,突然撤去外力F,此后杆cd仍然保持静止,杆ab做减速运动,直到速度减为零。已知从撤去外力F到杆ab速度减为零的过程中,杆ab沿斜面向上运动的距离
后金属杆cd刚要开始向上运动时,突然撤去外力F,此后杆cd仍然保持静止,杆ab做减速运动,直到速度减为零。已知从撤去外力F到杆ab速度减为零的过程中,杆ab沿斜面向上运动的距离![]() ,两杆的质量均为
,两杆的质量均为![]() ,接人电阻均为
,接人电阻均为![]() ,两杆与导轨间的动摩擦因数相同,且最大静摩擦力等于滑动摩擦力。重力加速度
,两杆与导轨间的动摩擦因数相同,且最大静摩擦力等于滑动摩擦力。重力加速度![]() 。试求:
。试求:
(1)在撤去外力F时,通过杆cd的电流大小和方向;
(2)在撤去外力F后金属杆ab速度减为零的过程中,杆ab上产生的内能;
(3)在0~4s内,外力F对杆ab的冲量大小。
【答案】(1)方向是由c沿杆指向d,2A;(2)1.1J;(3)6.8N·s。
【解析】
根据题意,先用右手定则判断电流的方向,然后受力分析,分析导体棒的运动情况。结合法拉第电磁感应电律求感应电动势,同时运用功能关系解决问题。
(1)在撤去外力F时,杆ab沿轨道向上运动,由右手定则可知,杆ab中电流方向由b沿杆指向a,所以杆cd中电流方向是由c沿杆指向d。
由题意知,开始两杆恰好不沿着轨道下滑,则有两杆沿斜面的滑动摩擦力等于最大静摩擦力即
![]()
当杆cd即将上滑时,设通过杆cd中电流大小为I,则
![]()
代入数据解得:
![]() ;
;
(2)设撤去外力F时,杆ab的速度为![]() ,产生的感应电动势为
,产生的感应电动势为![]() ,由法拉第电磁感应定律可知:
,由法拉第电磁感应定律可知:
![]()
又知:
![]()
解得:
![]()
从撤去外力F到杆ab速度减小为零的过程中,对杆ab由能量守恒定律可知:
![]()
所以,此过程中杆ab中产生的内能:
![]() ;
;
(3)设杆ab在力F作用下沿着轨道向上运动的匀加速的加速度为a,则
![]() ,
,
在某时刻![]() 的速度为v,则
的速度为v,则
![]()
杆ab所受安培力
![]()
对杆ab由牛顿第二定律得:
![]()
联立以上方程解得:
![]() (
(![]() )
)
由上式可知:力F随时间t成线性关系,当![]() 时,
时,
![]()
当![]() 时,
时,
![]()
所以,在0~4s内,力F对杆ab的冲量为:
![]() 。
。

 教材全解字词句篇系列答案
教材全解字词句篇系列答案