题目内容
16. 如图所示,光滑水平面上静止放着长L=2.0m质量M=3.0kg的木板,一个质量m=1.0kg的小物体(可视为质点)放在离木板右端a=0.4m处,m和M之间的动摩擦因数μ=0.1.今对木板施加向右的拉力F=10.0N,为使木板自物体下方分离出来,此拉力作用时间不得少于多长?
如图所示,光滑水平面上静止放着长L=2.0m质量M=3.0kg的木板,一个质量m=1.0kg的小物体(可视为质点)放在离木板右端a=0.4m处,m和M之间的动摩擦因数μ=0.1.今对木板施加向右的拉力F=10.0N,为使木板自物体下方分离出来,此拉力作用时间不得少于多长?
分析 木板要抽出,并不需要拉力一直作用到抽出,只需要作用到让M获得足够的速度,在拉力撤去后,能自己运动出来就行,因此,M的运动就分两个阶段,一:是在拉力和摩擦力作用下的加速阶段.二:是在摩擦力作用下的减速阶段.
解答 解:设拉力作用时间最少为t1抽出用的总时间为t,m做匀加速直线运动,M先做匀加速直线运动,后做匀减速直线运动,
则m的加速度大小 a1=$\frac{f}{m}=μg$
撤掉F前M的加速度大小a2=$\frac{F-f}{M}$,
撤掉F后M的加速度大小 a3=$\frac{f}{M}$,
$\frac{1}{2}{a}_{2}{{t}_{1}}^{2}+{a}_{2}{t}_{1}(t-{t}_{1})-\frac{1}{2}{a}_{3}(t-{t}_{1})^{2}$$-\frac{1}{2}{a}_{1}{t}^{2}$=d,
m与M速度相同时刚好抽出,则 a2t1-a3(t-t1)=a1t
由上两式可得:t1=0.80s
答:拉力作用时间不得少于0.80s.
点评 解决本题的关键理清整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,本题的误区是以为拉力要一直作用在M上,直到抽出为止.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.在光滑的水平面上,并排放着质量相等的物体A和B,并静止于水平面上,现用水平恒力F推A,此时沿F方向给B一个瞬时冲量I,当A追上B时,它们运动的时间是( )
| A. | $\frac{F}{2I}$ | B. | $\frac{I}{F}$ | C. | $\frac{2I}{F}$ | D. | $\frac{I}{2F}$ |
1. 如图所示,物块A、B在外力F的作用下一起沿水平地面做匀速直线运动的过程中,关于B与地面间的滑动摩擦力和A、B间的静摩擦力做功的说法,正确的是( )
如图所示,物块A、B在外力F的作用下一起沿水平地面做匀速直线运动的过程中,关于B与地面间的滑动摩擦力和A、B间的静摩擦力做功的说法,正确的是( )
 如图所示,物块A、B在外力F的作用下一起沿水平地面做匀速直线运动的过程中,关于B与地面间的滑动摩擦力和A、B间的静摩擦力做功的说法,正确的是( )
如图所示,物块A、B在外力F的作用下一起沿水平地面做匀速直线运动的过程中,关于B与地面间的滑动摩擦力和A、B间的静摩擦力做功的说法,正确的是( )| A. | 静摩擦力都做正功,滑动摩擦力都做负功 | |
| B. | 静摩擦力都不做功,滑动摩擦力都做负功 | |
| C. | 有静摩擦力做正功,有滑动摩擦力不做功 | |
| D. | 有静摩擦力做负功,有滑动摩擦力做正功 |
8.物理学的发展丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了物质生产的繁荣与人类文明的进步,下列表述正确的是( )
| A. | 牛顿发现了万有引力定律 | |
| B. | 牛顿通过实验证实了万有引力定律 | |
| C. | 丹麦的天文学家第谷提出了行星运动的三大定律,揭示了行星运动的规律 | |
| D. | 相对论的创立表明经典力学已不再适用 |
5.如图是一汽车在平直路面上启动的速度-时间图象,t1时刻起汽车的功率保持不变.由图象可知( )


| A. | 0~t1时间内,汽车的牵引力增大,加速度增大,功率增大 | |
| B. | 0~t1时间内,汽车的牵引力不变,加速度不变,功率减小 | |
| C. | t1~t2时间内,汽车的牵引力减小,加速度减小 | |
| D. | t1~t2时间内,汽车的牵引力不变,加速度减小 |
6.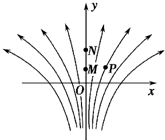 如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
 如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )| A. | M点的电势比P点的电势高 | |
| B. | 将负电荷由O点移动到P点,电场力做正功 | |
| C. | MN 两点间的电势差大于O、M两点间的电势差 | |
| D. | 在O点静止释放一带正电粒子,该粒子将沿y轴做加速直线运动 |
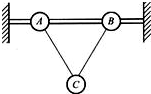 如图所示,A、B两小球固定在水平放置的细杆上,相距为l,两小球各用一根长也是l的细绳连接小球C,三个小球的质量都是m.则杆对小球A的作用力的大小为多大?(重力加速度为g)
如图所示,A、B两小球固定在水平放置的细杆上,相距为l,两小球各用一根长也是l的细绳连接小球C,三个小球的质量都是m.则杆对小球A的作用力的大小为多大?(重力加速度为g) 矩形导线框ADEC与水平面成30°角,磁感应强度为B=0.1特斯拉的匀强磁场垂直穿过整个线框平面.AC、DE长都为1米,电阻均为0.1欧,AD、CE部分足够长且电阻不计.质量为40克、电阻为0.2欧的金属棒MN平行DE边放在导线框上,并通过细绳与一个额定功率P=2瓦的电动机相连,电动机功率恒定,细绳与线框平面平行(如图所示).不计一切摩擦,g取10米/秒2.
矩形导线框ADEC与水平面成30°角,磁感应强度为B=0.1特斯拉的匀强磁场垂直穿过整个线框平面.AC、DE长都为1米,电阻均为0.1欧,AD、CE部分足够长且电阻不计.质量为40克、电阻为0.2欧的金属棒MN平行DE边放在导线框上,并通过细绳与一个额定功率P=2瓦的电动机相连,电动机功率恒定,细绳与线框平面平行(如图所示).不计一切摩擦,g取10米/秒2. 如图是一幅平抛物体与自由落体对比的频闪照片.
如图是一幅平抛物体与自由落体对比的频闪照片.