题目内容
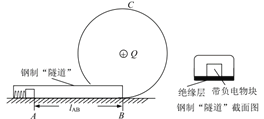
【题目】如图所示,单层光滑绝缘圆形轨道竖直放置,半径r=lm,其圆心处有一电荷量Q=+l×l0-4C 的点电荷,轨道左侧是一个钢制“隧道”,一直延伸至圆形轨道最低点B;在“隧道”底部辅设绝缘层。“隧道”左端固定一弹簧,用细线将弹簧与一静止物块拴接,初始状态弹簧被压缩,物块可看成质点,质量m=0.1kg,电荷量q=-![]() ×10-6C,与“隧道”绝缘层间的动摩擦因数μ=0.2。剪断细线,弹簧释放弹性势能Ep,促使物块瞬间获得初速度(忽略加速过程)。之后物块从A点沿直线运动至B点后沿圆形轨道运动,恰好通过最高点C。其中lAB=2m,设物块运动时电荷量始终不变,且不对Q的电场产生影响,不计空气阻力,静电力常量为k= 9.0×l09N·m2/C2。求:
×10-6C,与“隧道”绝缘层间的动摩擦因数μ=0.2。剪断细线,弹簧释放弹性势能Ep,促使物块瞬间获得初速度(忽略加速过程)。之后物块从A点沿直线运动至B点后沿圆形轨道运动,恰好通过最高点C。其中lAB=2m,设物块运动时电荷量始终不变,且不对Q的电场产生影响,不计空气阻力,静电力常量为k= 9.0×l09N·m2/C2。求:
(1)物块在最高点C时的速度大小;
(2)物块在圆形轨道最低点B时对轨道的压力大小;
(3)弹簧压缩时的弹性势能Ep和物块初速度vA。
【答案】(1) 4m/s (2) 6N (3) 3.2J, 8m/s
【解析】
(1)物块恰好通过最高点C,轨道对物块没有作用力,由牛顿第二定律得
![]()
其中
![]()
解得
vC=4m/s
(2)B→C过程,由动能定理得
![]()
解得
![]()
在B点,由牛顿第二定律得
![]()
解得
FNB=6N
根据牛顿第三定律知物块在圆形轨道最低点B时对轨道的压力大小 FNB′=FNB=6N。
(3)A→B,由动能定理得
![]()
又 f=μmg
解得
vA=8m/s
弹簧压缩时的弹性势能
![]()
解得
Ep=3.2J

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目