题目内容
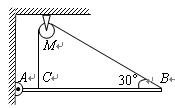
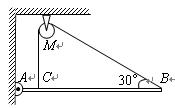
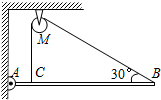 重为60N的均匀直杆AB一端用铰链与墙相连,另一端用一条通过定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=0.1AB.滑轮与绳重力不计.求:
重为60N的均匀直杆AB一端用铰链与墙相连,另一端用一条通过定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=0.1AB.滑轮与绳重力不计.求:(1)B点与C点处绳子的拉力TB、TC的大小.
(2)轴对定滑轮M的作用力大小.
分析:(1)因为B点与C点处绳子通过定滑轮相连,则拉力大小相等,对AB棒通过力矩平衡求出拉力的大小.
(2)定滑轮M通过两根绳子的拉力和轴对定滑轮的作用力处于平衡,根据共点力平衡求出轴对定滑轮M的作用力大小.
(2)定滑轮M通过两根绳子的拉力和轴对定滑轮的作用力处于平衡,根据共点力平衡求出轴对定滑轮M的作用力大小.
解答:解:(1)以A为固定转轴,AB棒力矩平衡:G?
=TC×0.1L+TB?Lsin30°①
绳子通过定滑轮,受力大小处处相等,即TB=TC②
可解得TB=TC=
G=50N③
(2)绕过定滑轮的绳子对滑轮的作用力沿两段绳的对角线方向,大小为F=TB?cos30°+TC?cos30°=50
N④
轴对定滑轮M的作用力FM与F的大小相等,方向相反,即FM=50
N⑤
答:(1)B点与C点处绳子的拉力大小分别为50N.
(2)轴对定滑轮M的作用力大小为50
N.
| L |
| 2 |

绳子通过定滑轮,受力大小处处相等,即TB=TC②
可解得TB=TC=
| 5 |
| 6 |
(2)绕过定滑轮的绳子对滑轮的作用力沿两段绳的对角线方向,大小为F=TB?cos30°+TC?cos30°=50
| 3 |
轴对定滑轮M的作用力FM与F的大小相等,方向相反,即FM=50
| 3 |
答:(1)B点与C点处绳子的拉力大小分别为50N.
(2)轴对定滑轮M的作用力大小为50
| 3 |
点评:本题考查了力矩平衡和共点力平衡问题,难度不大,关键能够正确地受力分析.

练习册系列答案
相关题目
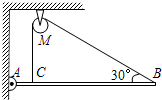 (2009?松江区二模)重为60N的均匀直杆AB一端用铰链与墙相连,另一端用一条通过定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=0.1AB.滑轮与绳重力不计.求:
(2009?松江区二模)重为60N的均匀直杆AB一端用铰链与墙相连,另一端用一条通过定滑轮M的绳子系住,如图所示,绳子一端与直杆AB的夹角为30°,绳子另一端在C点与AB垂直,AC=0.1AB.滑轮与绳重力不计.求: