题目内容
7.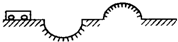 如图所示,质量m=2.0×104kg 的汽车以不 变的速率先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.如果桥面承受的压力不得超过3.0×105N,则:
如图所示,质量m=2.0×104kg 的汽车以不 变的速率先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.如果桥面承受的压力不得超过3.0×105N,则:(1)汽车允许的最大速率是多少?
(2)若以所求速度行驶,汽车对桥面的最小压力是多少?(g取10m/s2)
分析 汽车在最低点,靠支持力和重力的合力提供向心力,合力向上,支持力大于重力,在最高点,靠重力和支持力的合力提供向心力,合力向下,支持力小于重力,结合牛顿第二定律求出汽车允许的最大速率,以及在路面上行驶时的最小压力.
解答 解:(1)汽车在最低点受到的支持力最大,此时速度最大,根据牛顿定律得:
$N-mg=m\frac{{v}^{2}}{R}$
代入数据:$3×1{0}^{5}-2×1{0}^{5}=2×1{0}^{4}×\frac{{v}^{2}}{20}$
解得:v=10m/s.
(2)当汽车运动到最高点时,支持力最小,根据牛顿第二定律得:
$mg-N′=m\frac{{v}^{2}}{R}$
代入数据:$2×1{0}^{5}-N′=2×1{0}^{4}×\frac{100}{20}$,
解得:N′=1.0×105N.
根据牛顿第三定律得,汽车对桥面的最小压力为:N″=N′=1.0×105N.
答:(1)汽车允许的最大速率是10m/s;
(2)若以所求速度行驶,汽车对桥面的最小压力是1.0×105N.
点评 解决本题的关键知道向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
10.正在运转的洗衣机,当脱水桶转得很快时,机身振动并不强烈,而切断电源,转动逐渐减慢直到停下来的过程中,在某一时刻t时,机身反而会发生强烈振动,此后脱水桶转速继续减慢,机身的振动也随之减弱,这种现象说明( )
| A. | 转动逐渐减慢过程中驱动力的频率不变 | |
| B. | 转动逐渐减慢过程中驱动力的频率增大 | |
| C. | t时刻驱动力的频率等于洗衣机的固有频率 | |
| D. | t时刻脱水桶的惯性最大 |
2. 质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定于其左端,另一质量也为m的物块乙以4m/s的速度与甲相向运动,如图所示.则( )
质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定于其左端,另一质量也为m的物块乙以4m/s的速度与甲相向运动,如图所示.则( )
 质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定于其左端,另一质量也为m的物块乙以4m/s的速度与甲相向运动,如图所示.则( )
质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定于其左端,另一质量也为m的物块乙以4m/s的速度与甲相向运动,如图所示.则( )| A. | 甲、乙两物块在弹簧压缩过程中,由于弹力属于内力作用,故系统动量守恒 | |
| B. | 当两物块相距最近时,甲物块的速率为零 | |
| C. | 甲物块的速率可能达到5m/s | |
| D. | 当甲物块的速率为1m/s时,乙物块的速率可能为2m/s,也可能为0 |
12.下列说法中正确的是( )
| A. | 录音机在磁带上录制声音时,利用了电磁感应原理 | |
| B. | 日光灯的工作原理是自感现象 | |
| C. | 金属中的涡流会产生热量,生活中的电磁炉是利用这原理而工作的 | |
| D. | 电动机的工作原理是运动产生电流 |
19. 如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
 如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )| A. | 摆长约为10 cm | |
| B. | 发生共振时单摆的周期为1 s | |
| C. | 若增大摆长,共振曲线的“峰”将向右移动 | |
| D. | 若增大摆长,共振曲线的“峰”将向左移动 |
16.在力学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 伽利略发现了行星运动的规律 | |
| B. | 卡文迪许通过实验测出了静电力恒量 | |
| C. | 牛顿最早指出力不是维持物体运动的原因 | |
| D. | 笛卡尔对牛顿第一定律的建立做出了贡献 |
17.下列说法正确的是( )
| A. | 感应电流的磁场方向总是与引起感应电流的磁场方向相反 | |
| B. | 感应电流的磁场方向总是与引起感应电流的磁场方向相同 | |
| C. | 楞次定律只能判断闭合回路中感应电流的方向,不能判断感应电动势的正负极性 | |
| D. | 楞次定律表明感应电流的效果总是与引起感应电流的原因相对抗 |
 如图:一个重力不计,质量为m,电量为+q的电荷在场强为E的匀强电场中,从B运动到A,在B点速度为V0,到A点速度恰好为零,则该电荷电势能变化了$\frac{1}{2}{mv}_{0}^{2}$,A、B两点电势差UAB=$\frac{{mv}_{0}^{2}}{2q}$,电荷从B运动到A,电场力作负功.
如图:一个重力不计,质量为m,电量为+q的电荷在场强为E的匀强电场中,从B运动到A,在B点速度为V0,到A点速度恰好为零,则该电荷电势能变化了$\frac{1}{2}{mv}_{0}^{2}$,A、B两点电势差UAB=$\frac{{mv}_{0}^{2}}{2q}$,电荷从B运动到A,电场力作负功.