题目内容
在用单摆测重力加速度的实验中,测得单摆摆角小于5°时,完成n次全振动时间为t,用毫米刻度尺测得摆线长为l,用游标卡尺测得摆球直径为d.
(1)测得重力加速度的表达式为g=
.
(2)完成50次全振动时停表记录的时间t=
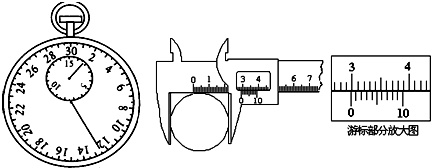
(3)游标卡尺的读数如图所示,摆球直径d=
(4)实验中某学生所测g值偏大,其原因可能是
A.实验室离海平面太高
B.摆球太重
C.测出n次全振动时间为t,误作为(n+1)次全振动时间进行计算
D.以摆线长与摆球直径之和作为摆长来计算.
(1)测得重力加速度的表达式为g=
4n2π2(l+
| ||
| t2 |
4n2π2(l+
| ||
| t2 |
(2)完成50次全振动时停表记录的时间t=
102.5
102.5
s.(3)游标卡尺的读数如图所示,摆球直径d=
29.8
29.8
mm.(4)实验中某学生所测g值偏大,其原因可能是
CD
CD
.A.实验室离海平面太高
B.摆球太重
C.测出n次全振动时间为t,误作为(n+1)次全振动时间进行计算
D.以摆线长与摆球直径之和作为摆长来计算.

分析:(1)由单摆的周期公式即可求解;
(2)秒表分针与秒针示数之和是秒表示数;
(3)考查游标卡尺和秒表的读数:先读主尺(只读整数),再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读);
(4)根据单摆周期公式列式分析即可.
(2)秒表分针与秒针示数之和是秒表示数;
(3)考查游标卡尺和秒表的读数:先读主尺(只读整数),再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读);
(4)根据单摆周期公式列式分析即可.
解答:解:(1)根据题意可知:T=
,
由单摆的周期公式T=2π
,
有效长度L=l+
解得:g=
.
(2)由图示秒表可知,秒表示数为90s+12.5=102.5s.
(3)主尺:29mm,游标尺对齐格数:8个格,读数8×0.1=0.8mm,所以直径为29+0.8=29.8mm
(4)A、高度越高,重力加速度越小.实验室离海平面太高,g值偏小,故A错误;
B、摆球的质量不影响单摆的周期,所以不影响测量的重力加速度的值.故B错误;
C、将振动次数n错记为(n+1),单摆的周期T=
,周期的测量值偏小,
根据g=
,测算的g值比实际值大,故C正确;
D、以摆线长加小球直径作为摆长来计算了,测得摆长偏大,则测得的重力加速度偏大.故D正确.
故选:CD.
故答案为:(1)
;(2)102.5;(3)29.8;(4)CD.
| t |
| n |
由单摆的周期公式T=2π
|
有效长度L=l+
| d |
| 2 |
解得:g=
4n2π2(l+
| ||
| t2 |
(2)由图示秒表可知,秒表示数为90s+12.5=102.5s.
(3)主尺:29mm,游标尺对齐格数:8个格,读数8×0.1=0.8mm,所以直径为29+0.8=29.8mm
(4)A、高度越高,重力加速度越小.实验室离海平面太高,g值偏小,故A错误;
B、摆球的质量不影响单摆的周期,所以不影响测量的重力加速度的值.故B错误;
C、将振动次数n错记为(n+1),单摆的周期T=
| t |
| n |
根据g=
| 4π2L |
| T2 |
D、以摆线长加小球直径作为摆长来计算了,测得摆长偏大,则测得的重力加速度偏大.故D正确.
故选:CD.
故答案为:(1)
4n2π2(l+
| ||
| t2 |
点评:常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度并进行误差分析.

练习册系列答案
相关题目
 在“用单摆测重力加速度”的实验中,
在“用单摆测重力加速度”的实验中,