题目内容
如图14所示,倾角为α的光滑斜面与半径为R=0.4 m半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4 m,直径CD沿竖直方向,C、E可看做重合。现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的![]() 。(取g=10 m/s2)求:
。(取g=10 m/s2)求:
(1)若要使小球经E处水平进入圆形轨道且能沿轨道运动,H至少要有多高?如小球恰能沿轨道运动,那么小球在水平面DF上能滑行多远?
(2)若小球静止释放处离B点的高度h小于(1)中H的最小值,小球可击中与圆心等高的G点,求此h的值。

图14
解:.解析:(1)小球从光滑斜面轨道下滑,机械能守恒,设到达B点时的速度大小为v,则
mgH=![]() mv2
mv2
因为小球在水平面所受阻力为其重力的![]() ,
,
根据牛顿第二定律a=![]() =2 m/s2。
=2 m/s2。
vE2-v2=-2aL
小球能在竖直平面内做圆周运动,在圆形轨道最高点必须满足:
mg≤m![]()
联立以上几式并代入数据得:H≥0.28 m
小球恰能沿轨道运动,根据动能定理:
mg·2R-kmg·x=0-![]() mvE2,x=5 m。
mvE2,x=5 m。
(2)若h<H,小球过E点后做平抛运动,设球经E点时的速度大小为vx,则击中半圆中点G时:
竖直方向:R=![]() gt2
gt2
水平方向:R=vxt
由动能定理:mgh-kmgL=![]() mvx2
mvx2
联立以上三式并代入数据得h=0.18 m。

练习册系列答案
相关题目
 如图14所示,一带电量为q=-5×10-3 C,质量为m=0.1kg的小物块处于一倾角为θ=37°的光滑绝缘斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.(g取10m/s2):
如图14所示,一带电量为q=-5×10-3 C,质量为m=0.1kg的小物块处于一倾角为θ=37°的光滑绝缘斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.(g取10m/s2):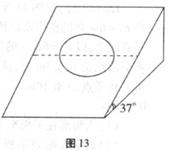


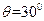 的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住,已知人的质量m=60kg,小车的质量M=10kg,绳及滑轮的质量,滑轮与绳间的摩擦均不计,斜面与小车间的滑动摩擦因数为
的固定斜面上,跨过定滑轮的轻绳一端系在小车的前端,另一端被坐在小车上的人拉住,已知人的质量m=60kg,小车的质量M=10kg,绳及滑轮的质量,滑轮与绳间的摩擦均不计,斜面与小车间的滑动摩擦因数为 ,斜面足够长,当人以280N
,斜面足够长,当人以280N 的力拉绳时,求:
的力拉绳时,求: