题目内容
 如图14所示,一带电量为q=-5×10-3 C,质量为m=0.1kg的小物块处于一倾角为θ=37°的光滑绝缘斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.(g取10m/s2):
如图14所示,一带电量为q=-5×10-3 C,质量为m=0.1kg的小物块处于一倾角为θ=37°的光滑绝缘斜面上,当整个装置处于一水平向左的匀强电场中时,小物块恰处于静止状态.(g取10m/s2):(1)求电场强度多大?
(2)若从某时刻开始,电场强度减小为原来的
| 1 | 2 |
分析:(1)小物块受到重力、电场力和支持力而处于静止状态,根据平衡条件求解电场强度.
(2)当电场强度减小为原来的
时,物块将沿斜面匀加速下滑,重力做正功,电场力做负功,根据动能定理求解速度大小.
(2)当电场强度减小为原来的
| 1 |
| 2 |
解答:解:(1)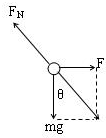 小物块受力如图,则
小物块受力如图,则
电场力F=mgtanθ
又F=qE
得到E=
=1.5×102N/C
(2)当电场强度减小为原来的
时,根据动能定理得
mgLsinθ-q
ELcosθ=
mv2
代入解得 v=3m/s
答:(1)电场强度为1.5×10-5N/C.
(2)若从某时刻开始,电场强度减小为原来的
,物块下滑距离L=1.5m时的速度大小为3m/s.
 小物块受力如图,则
小物块受力如图,则电场力F=mgtanθ
又F=qE
得到E=
| mgtanθ |
| q |
(2)当电场强度减小为原来的
| 1 |
| 2 |
mgLsinθ-q
| 1 |
| 2 |
| 1 |
| 2 |
代入解得 v=3m/s
答:(1)电场强度为1.5×10-5N/C.
(2)若从某时刻开始,电场强度减小为原来的
| 1 |
| 2 |
点评:本题是电场中物体平衡问题,根据力学的解题方法和思路进行分析研究.其中电场力是关键,它是联系力学与电场的桥梁.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




