题目内容
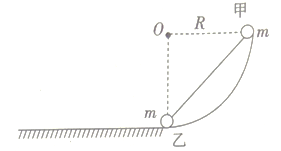
【题目】如图所示,足够长的半径为R=0.4m的![]() 圆弧形光滑轨道固定于竖直平面内,圆孤形轨道与光滑固定的水平轨道相切,可视为质点的质量均为m=0.5kg的小球甲、乙用轻杆连接,置于圆弧形轨道上,小球甲与O点等高,小球乙位于圆心O的正下方。某时刻将两小球由静止释放,最终它们在水平面上运动。g取10m/s2。则( )
圆弧形光滑轨道固定于竖直平面内,圆孤形轨道与光滑固定的水平轨道相切,可视为质点的质量均为m=0.5kg的小球甲、乙用轻杆连接,置于圆弧形轨道上,小球甲与O点等高,小球乙位于圆心O的正下方。某时刻将两小球由静止释放,最终它们在水平面上运动。g取10m/s2。则( )
A. 下滑过程中小球乙的机械能守恒
B. 两小球最终在水平面上运动的速度大小为2![]() m/s
m/s
C. 当小球甲滑到圆轨道最低点时,轨道对它的支持力大小为10N
D. 小球甲下滑过程中重力对它做功的功率增大
【答案】C
【解析】
下滑过程中,杆要对小球乙做功,则小球乙的机械能不守恒,选项A错误;两个球系统机械能守恒,故:mgR=![]() mv2+
mv2+![]() mv2,解得:
mv2,解得:![]() ,故B错误;小球甲下滑到圆弧形轨道最低点,重力和支持力的合力提供向心力,N-mg=m
,故B错误;小球甲下滑到圆弧形轨道最低点,重力和支持力的合力提供向心力,N-mg=m![]() ,解得:N=mg+
,解得:N=mg+![]() =0.5×10+0.5×
=0.5×10+0.5×![]() =10N,根据牛顿第三定律,压力也为10N,故C正确;小球甲下滑过程中,最高点速度为零,故重力的功率为零;最低点速度和重力垂直,故重力的功率也是零;而中途重力的功率不为零,故重力的功率应该时先增加后减小,故D错误;故选C。
=10N,根据牛顿第三定律,压力也为10N,故C正确;小球甲下滑过程中,最高点速度为零,故重力的功率为零;最低点速度和重力垂直,故重力的功率也是零;而中途重力的功率不为零,故重力的功率应该时先增加后减小,故D错误;故选C。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目