题目内容
(13分)如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究,已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,绳子不可伸长,如果m= ,求:
,求:

⑴物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值;
⑵系统由静止释放后运动过程中物体C对B的拉力.
【答案】
⑴3;⑵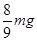 。
。
【解析】
试题分析:⑴因为绳子不可伸长,因此,对物体A、B、C整体,具有了相同大小的加速度a,根据牛顿第二定律有:mg=(2M+m)a
由题意知:m=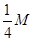
联立两式解得:a=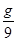
设物体B从静止开始下落h高度时所用时间为t1,自由落体下落h高度时所用时间为t2,根据匀变速直线运动和自由落体运动规律有:h=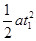 =
=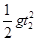
解得: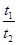 =
=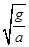 =3
=3
对C,受重力mg和物体B的拉力T作用,根据牛顿第二定律有:mg-T=ma
根据牛顿第三定律可知,物体C对B的拉力为:T′=T
联立以上各式解得:T′=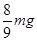
考点:本题主要考查了匀变速直线运动、自由落体运动规律、牛顿第二定律的应用,以及整体法与隔离法的灵活运用问题,属于中档题。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目

 神舟十号在酒泉卫星发射中心“921工位”,2013年6月11日17时38分,由长征二号F改进型运载火箭(遥十)“神箭”成功发射.在轨飞行十五天左右,加上发射与返回,其中停留天宫一号十二天,6月13日与天宫一号进行对接..假如神舟十号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )
神舟十号在酒泉卫星发射中心“921工位”,2013年6月11日17时38分,由长征二号F改进型运载火箭(遥十)“神箭”成功发射.在轨飞行十五天左右,加上发射与返回,其中停留天宫一号十二天,6月13日与天宫一号进行对接..假如神舟十号与天宫一号对接前所处的轨道如图所示,当它们处于如图所示的轨道运行时,下列说法正确的是( )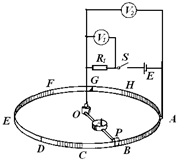 如图所示的电路中,直径为D的圆环是用粗细均匀的电阻丝制成的,其阻值为R,图中A,B,…,H为圆环的等分点,A点固定,P为滑片,且滑片P能沿圆环滑动,并保持良好的接触,电源电动势为E,内阻不计.当闭合电键S后,滑片P沿圆环顺时针滑动时,图中各表的示数会发生变化.甲、乙两同学按此电路图,分别做实验,并记下当滑片P在某些位置时各电表的示数.
如图所示的电路中,直径为D的圆环是用粗细均匀的电阻丝制成的,其阻值为R,图中A,B,…,H为圆环的等分点,A点固定,P为滑片,且滑片P能沿圆环滑动,并保持良好的接触,电源电动势为E,内阻不计.当闭合电键S后,滑片P沿圆环顺时针滑动时,图中各表的示数会发生变化.甲、乙两同学按此电路图,分别做实验,并记下当滑片P在某些位置时各电表的示数. 2011年5月15日,国际田联110m栏钻石联赛上海站敲响战鼓,冠军争夺在刘翔和奥利弗之间展开.比赛临近结束,选手全力冲刺时,观众看到如图所示的场景,齐声欢呼“刘翔最快”;很快,根据表中所示的比赛成绩,裁判裁定刘翔获胜,观众和裁判判断刘翔快过奥利弗的方法分别是( )
2011年5月15日,国际田联110m栏钻石联赛上海站敲响战鼓,冠军争夺在刘翔和奥利弗之间展开.比赛临近结束,选手全力冲刺时,观众看到如图所示的场景,齐声欢呼“刘翔最快”;很快,根据表中所示的比赛成绩,裁判裁定刘翔获胜,观众和裁判判断刘翔快过奥利弗的方法分别是( )
