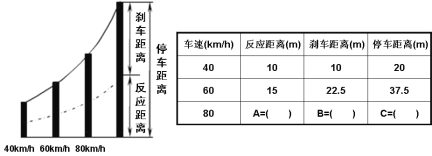
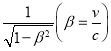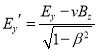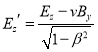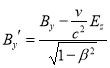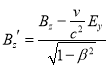题目内容
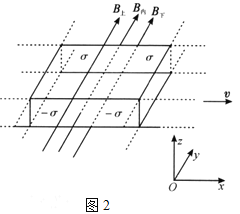
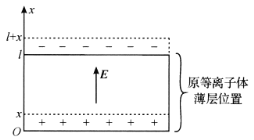
【题目】当温度从低到高变化时,通常物质会经历固体、液体和气体三种状态,当温度进一步升高,气体中的原子、分子将出现电离,形成电子、离子组成的体系,这种由大量带电粒子(有时还有中性粒子)组成的体系便是等离子体.等离子体在宏观上具有强烈保持电中性的趋势,如果由于某种原因引起局部的电荷分离,就会产生等离子体振荡现象.其原理如图,考虑原来宏观电中性的、厚度为![]() 的等离子体薄层,其中电子受到扰动整体向上移动一小段距离
的等离子体薄层,其中电子受到扰动整体向上移动一小段距离![]() ,这样在上、下表面就可分别形成厚度均为
,这样在上、下表面就可分别形成厚度均为![]() 的负、正电薄层,从而在中间宏观电中性区域形成匀强电场
的负、正电薄层,从而在中间宏观电中性区域形成匀强电场![]() ,其方向已在图中示出.设电子电量为
,其方向已在图中示出.设电子电量为![]() 、质量为
、质量为![]() 、数密度(即单位体积内的电子数目)为
、数密度(即单位体积内的电子数目)为![]() ;并设如下各问中,电荷运动及电场变化所激发的磁场及磁相互作用均可忽略不计
;并设如下各问中,电荷运动及电场变化所激发的磁场及磁相互作用均可忽略不计
(1)试求该匀强电场的大小![]() .(可利用平行板电容器公式:
.(可利用平行板电容器公式:![]() ,其中
,其中![]() 为真空介电常量,
为真空介电常量,![]() 为电容器极板面积,
为电容器极板面积,![]() 为极板间距)
为极板间距)
(2)假定此后电子保持整体运动,且其运动对正离子的反冲及其与正离子之间的碰撞均可忽略不计.试说明这种整体运动为简谐振动,并求解振动角频率![]() 的表达式.(结果以参量
的表达式.(结果以参量![]() 、
、![]() 、
、![]() 、
、![]() 表述)
表述)
(3)在上图原等离子体薄层所在区域及其周边施加![]() 方向交变外电场
方向交变外电场![]() ,其中
,其中![]() 、
、![]() 为已知常量.忽略正离子的运动,但考虑因电子与正离子的碰撞所带来的能量损耗,其效果可以等价为平均作用于每个电子上的线性速度阻尼力
为已知常量.忽略正离子的运动,但考虑因电子与正离子的碰撞所带来的能量损耗,其效果可以等价为平均作用于每个电子上的线性速度阻尼力![]() ,其中
,其中![]() 为已知常量
为已知常量
①仍假定此后电子保持整体运动,且其稳态振动振幅![]() ,试求该振幅
,试求该振幅![]() ;
;
②将等离子体看作是一种电介质,即将交变电场作用下等离子体内部正、负电荷的相对移位看作是“极化”效应,试求解如上交变电场中等离子体薄层对应的复相对介电常量![]()
【答案】(1) ![]() (2)
(2) 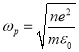 (3)①
(3)①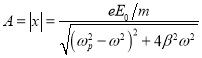 ②
②![]()
【解析】
(1)设等离子体上下底面积为![]() ,则下表面电荷宏观电量为
,则下表面电荷宏观电量为![]() ’
’
匀强电场场强大小为![]() .
.
(2)电子整体运动可由单个电子代表.处于题图中宏观电中性区域内的自由电子受力为
![]()
其中![]() 也是该电子相对原平衡位置的位移,即该电子运动满足
也是该电子相对原平衡位置的位移,即该电子运动满足![]() .
.
因此,以该电子代表的整体运动为简谐振动,其角频率为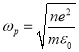 .
.
(3)①取交变外电场复表述![]()
则单电子稳态振动对应的复表述为
![]() , ①
, ①
其中![]() 为复振幅.
为复振幅.
单电子稳态振动复表述满足方程![]() ,
,
其中![]() 为(2)问所求.上式可化为
为(2)问所求.上式可化为![]() .
.
将①式代入得![]() ,
,
![]() , ②
, ②
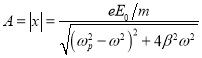 ,
,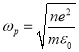 .
.
②解法一:定义等离子体介质的极化强度矢量![]() 为单位体积内微观电偶极矩的求和,则由题文可知,当电子相对正离子整体移位
为单位体积内微观电偶极矩的求和,则由题文可知,当电子相对正离子整体移位![]() 时(
时(![]() 为
为![]() 轴方向的单位向量),有
轴方向的单位向量),有
![]() .
.
由(1)问中结果,得其产生附加电场为![]() .
.
对题文所述交变外电场作用下的极化机制,采用复表述并投影到![]() 轴方向,即得
轴方向,即得
![]() ,
,![]() . ③
. ③
由线性极化规律有![]()
其中![]() 为复电极化率.代入③式得
为复电极化率.代入③式得![]() ,即
,即![]() .
.
代入②式得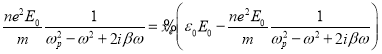 .
.
将 代入,有
代入,有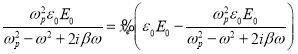 ,
,
解得![]() ,
,
故得复相对介电常量为![]() ,
,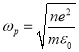 .
.
解法二:由总电场复表述![]()
求解稳态振动复表述(仍设![]() )方程
)方程
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
得![]() ,
,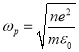 .
.