题目内容
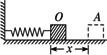
一弹簧的劲度系数为k，把弹簧的一端固定，另一端连接一个物体，如图所示．若O点是弹簧自由伸长时物体所在的位置，试求当弹簧的伸长量(或压缩量)为x时，弹簧的弹性势能为多少？
答案：
解析：
解析：
|
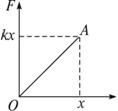
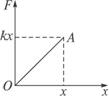
解析：本题中，可以认为物体初末动能为零，克服弹簧弹力做的功就等于弹簧势能的增量，由于弹力是变力，我们可以作出弹力随弹簧伸长(或压缩)的图象，由图象面积来求出弹力的功，即可得出弹簧势能的变化，即末状态弹性势能的大小． 根据胡克定律，弹力的大小跟弹簧的伸长量成正比，即F＝－kx 负号表示F与伸长的方向相反，显然，弹力做功是变力做功，可用示功图来求弹力所做的功，作出Fx图如图所示．由图可知：
弹力所做的功的大小等于△OAx的面积，即W＝ 由功能关系可知：弹簧伸长量(或压缩量)为x时，弹簧的弹性势能Ep＝ 方法归纳 意此处空半格弹性势能的变化可以由弹力做功来量度．本题中弹簧的弹性势能就等于弹簧从该位置回到原长时弹性势能的变化，即可用弹力所做的功来量度． 弹簧弹力F大小与位移x成正比，还可用平均力代替求功 W＝Fx＝k· |
kx·x＝
练习册系列答案
相关题目
在水平地面上运动的小车车厢底部有一质量为m1的木块，木块和车厢通过一根水平轻弹簧相连接，弹簧的劲度系数为k．在车厢的顶部用一根细线悬挂一质量为m2的小球．某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢保持相对静止，弹簧的形变量为X，如图所示．不计木块与车厢底部的摩擦力，则在这段时间内（ ）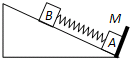
如图，一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M，物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上．现用外力沿斜面向下缓慢推动物块B，当弹簧具有5J的弹性势能时撤去推力，释放物块B．已知物块A、B的质量分别为5kg和10kg，弹簧的弹性势能的表达式为
