题目内容
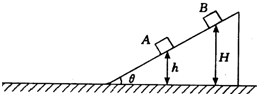 如图所示,倾角θ=30°的光滑斜面固定于光滑水平面上,斜面与水平面的连接处是光滑圆弧,在斜面上距水平面高分别为h=0.2m和H=0.8m的两个位置同时由静止释放两个物体A和B(均可看成质点).g取10m/s2,求:
如图所示,倾角θ=30°的光滑斜面固定于光滑水平面上,斜面与水平面的连接处是光滑圆弧,在斜面上距水平面高分别为h=0.2m和H=0.8m的两个位置同时由静止释放两个物体A和B(均可看成质点).g取10m/s2,求:(1)A、B两物体滑到水平面时的速度大小vA和vB;
(2)从开始释放A、B两物体到B物体追上A物体所用的总时间t.
分析:(1)求AB两物体滑到水平面上的速度,分别利用动能定理即可求得;
(2)由牛顿第二定律求出物体在斜面上的加速度,利用运动学公式求出在斜面上的时间,当物体在水平面上匀速运动时,要想追上,在水平面上运动的位移相等,故可求的时间.
(2)由牛顿第二定律求出物体在斜面上的加速度,利用运动学公式求出在斜面上的时间,当物体在水平面上匀速运动时,要想追上,在水平面上运动的位移相等,故可求的时间.
解答:解:(1)设A物体的质量为m,B物体的质量为M,A、B两物体下滑过程机械能守恒:
mgh=
m
解得vA=
=
m/s=2m/s
MgH=
M
解得:vB=
=
m/s=4m/s
(2)设A、B两物体下滑的时间分别为tA、tB,由牛顿第二定律求得A、B两物体下滑的加速度均为:
a=gsinθ
由运动学公式:vA=atA vB=atB
代入数据解得:tA=0.4s tB=0.8s
在水平面上两物体均做匀速直线运动,所以当B物体追上A物体时,有
vA(t-tA)=vB(t-tB)
代入数据解得:t=1.2s
答:(1)A、B两物体滑到水平面时的速度大小vA为2m/s和vB为4m/s;
(2)从开始释放A、B两物体到B物体追上A物体所用的总时间t为1.2s.
mgh=
| 1 |
| 2 |
| v | 2 A |
解得vA=
| 2gh |
| 2×10×0.2 |
MgH=
| 1 |
| 2 |
| v | 2 B |
解得:vB=
| 2gH |
| 2×10×0.8 |
(2)设A、B两物体下滑的时间分别为tA、tB,由牛顿第二定律求得A、B两物体下滑的加速度均为:
a=gsinθ
由运动学公式:vA=atA vB=atB
代入数据解得:tA=0.4s tB=0.8s
在水平面上两物体均做匀速直线运动,所以当B物体追上A物体时,有
vA(t-tA)=vB(t-tB)
代入数据解得:t=1.2s
答:(1)A、B两物体滑到水平面时的速度大小vA为2m/s和vB为4m/s;
(2)从开始释放A、B两物体到B物体追上A物体所用的总时间t为1.2s.
点评:本题主要抓住物体在水平面上相遇时在水平面上通过的位移相等即可求得.

练习册系列答案
相关题目
 如图所示,倾角为37°斜面上方有一小球以一定的速度水平抛出,在空中飞行2s后恰好垂直撞在斜面上,sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示,倾角为37°斜面上方有一小球以一定的速度水平抛出,在空中飞行2s后恰好垂直撞在斜面上,sin37°=0.6,cos37°=0.8,g=10m/s2.求: 如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,物体向左最多能滑到传送带左右两端AB的中点处,重力加速度g=10m/s2,求:
如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,物体向左最多能滑到传送带左右两端AB的中点处,重力加速度g=10m/s2,求: (2007?徐州一模)如图所示,倾角θ=37゜的传送带AB长L=20m,以v=5m/s速度沿顺时针方向匀速转动.质量M=lkg的木块由AB的中点c从静止开始下滑,0.5s后被一颗质量 m=20g的子弹以速度v0=500m/s沿传送带向上正对射入,子弹穿出时的速度u=200m/s.以后每隔1.5s就有一颗质量和速度相同的子弹射人木块.设子弹射穿木块的时间极短,且每次射人时木块对子弹的阻力相同.已知木块与传送带间的动摩擦因数μ=0.25,sin37゜=0.60,cos37゜=O.80,g取lOm/s2.求:
(2007?徐州一模)如图所示,倾角θ=37゜的传送带AB长L=20m,以v=5m/s速度沿顺时针方向匀速转动.质量M=lkg的木块由AB的中点c从静止开始下滑,0.5s后被一颗质量 m=20g的子弹以速度v0=500m/s沿传送带向上正对射入,子弹穿出时的速度u=200m/s.以后每隔1.5s就有一颗质量和速度相同的子弹射人木块.设子弹射穿木块的时间极短,且每次射人时木块对子弹的阻力相同.已知木块与传送带间的动摩擦因数μ=0.25,sin37゜=0.60,cos37゜=O.80,g取lOm/s2.求: (2006?松江区二模)如图所示,倾角θ=30°、宽度L=1m的足够长为U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1Ω、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦).问:
(2006?松江区二模)如图所示,倾角θ=30°、宽度L=1m的足够长为U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1Ω、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦).问: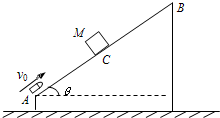 如图所示,倾角θ=37°的固定斜面AB长L=18.4m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=500m/s沿斜面向上的速度正对射入并穿出,穿出速度u=200m/s.以后每隔1.0s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37°=0.80,求:
如图所示,倾角θ=37°的固定斜面AB长L=18.4m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=500m/s沿斜面向上的速度正对射入并穿出,穿出速度u=200m/s.以后每隔1.0s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37°=0.80,求: