题目内容
9.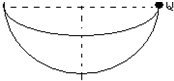 质量为m的滑块从固定在平面上、半径为R的半球形碗的边缘由静止滑向碗底,经过碗底时的速度为v,若滑块与碗之间的动摩擦因数为μ,求:
质量为m的滑块从固定在平面上、半径为R的半球形碗的边缘由静止滑向碗底,经过碗底时的速度为v,若滑块与碗之间的动摩擦因数为μ,求:①在碗底位置时滑块的向心加速度是多大?
②碗底对滑块的压力是多大?
③在过碗底时滑块受到摩擦力的大小.
分析 ①由公式${a_n}=\frac{v^2}{R}$求向心加速度.
②滑块经过碗底时,由重力和碗底对球支持力的合力提供向心力,根据牛顿第二定律求出碗底对球的支持力,由牛顿第三定律得到压力.
③再由摩擦力公式求解在过碗底时滑块受到摩擦力的大小.
解答 解:①在碗底位置时滑块的向心加速度大小为:${a_n}=\frac{v^2}{R}$
②由牛顿第二定律得:${F_N}-mg=m\frac{v^2}{R}$
得 ${F_N}=m(g+\frac{v^2}{R})$
由牛顿第三定律得:碗底对滑块的压力是 FN′=FN=m(g+$\frac{{v}^{2}}{R}$)
③在过碗底时滑块受到摩擦力大小为:$f=μ{F_N}=μm(g+\frac{v^2}{R})$
答:
①在碗底位置时滑块的向心加速度是$\frac{{v}^{2}}{R}$.
②碗底对滑块的压力是m(g+$\frac{{v}^{2}}{R}$).
③在过碗底时滑块受到摩擦力的大小是μm(g+$\frac{{v}^{2}}{R}$).
点评 解决本题的关键确定物体做圆周运动向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.甲、乙两根圆柱体金属丝均为同种材料制成,直径分别是d1=0.5mm和d2=1mm,长度分别为L1=20cm,L2=10cm,它们的电阻之比为( )
| A. | 1:1 | B. | 4:1 | C. | 8:1 | D. | 1:4 |
20.下列说法正确的是( )
| A. | 在黑体辐射中,随着温度的升高,辐射强度的极大值向波长较短的方向移动 | |
| B. | 汤姆生发现了电子,并提出原子的核式结构模型 | |
| C. | 核子结合成原子核一定有质量亏损,并释放出能量 | |
| D. | 太阳内部发生的核反应是热核反应 |
4. 中国舰载机歼-15飞机在我国第一艘航母“辽宁舰”上顺利完成起降飞行训练.若舰载机起飞速度是60m/s,起飞仰角是14°,则舰载机起飞时的水平速度和竖直速度大小是(取sin14°=0.24,cos14°=0.97)( )
中国舰载机歼-15飞机在我国第一艘航母“辽宁舰”上顺利完成起降飞行训练.若舰载机起飞速度是60m/s,起飞仰角是14°,则舰载机起飞时的水平速度和竖直速度大小是(取sin14°=0.24,cos14°=0.97)( )
 中国舰载机歼-15飞机在我国第一艘航母“辽宁舰”上顺利完成起降飞行训练.若舰载机起飞速度是60m/s,起飞仰角是14°,则舰载机起飞时的水平速度和竖直速度大小是(取sin14°=0.24,cos14°=0.97)( )
中国舰载机歼-15飞机在我国第一艘航母“辽宁舰”上顺利完成起降飞行训练.若舰载机起飞速度是60m/s,起飞仰角是14°,则舰载机起飞时的水平速度和竖直速度大小是(取sin14°=0.24,cos14°=0.97)( )| A. | 14.4 m/s 58.2m/s | B. | 58.2m/s 14.4 m/s | ||
| C. | 8.4 m/s 42.8 m/s | D. | 42.8 m/s 8.4 m/s |
14.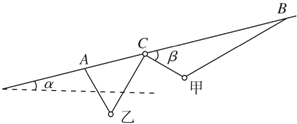 如图所示,一固定的细直杆与水平面的夹角为α=150,一个小轻环C(质量忽略不计)套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°,不计一切摩擦.则小环甲与小环乙的质量比m甲:m乙等于( )
如图所示,一固定的细直杆与水平面的夹角为α=150,一个小轻环C(质量忽略不计)套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°,不计一切摩擦.则小环甲与小环乙的质量比m甲:m乙等于( )
 如图所示,一固定的细直杆与水平面的夹角为α=150,一个小轻环C(质量忽略不计)套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°,不计一切摩擦.则小环甲与小环乙的质量比m甲:m乙等于( )
如图所示,一固定的细直杆与水平面的夹角为α=150,一个小轻环C(质量忽略不计)套在直杆上,一根轻质细线的两端分别固定于直杆上的A、B两点,细线依次穿过小环甲、小轻环C和小环乙,且小环甲和小环乙分居在小轻环C的两侧.调节A、B间细线的长度,当系统处于静止状态时β=45°,不计一切摩擦.则小环甲与小环乙的质量比m甲:m乙等于( )| A. | tan15° | B. | tan30° | C. | tan60° | D. | l |
9.如图所示是甲、乙两物体运动的v-t 图象,其加速度大小关系是( )


| A. | a甲<a乙 | B. | a甲﹦a乙 | C. | a甲>a乙 | D. | 无法比较 |

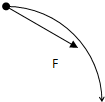

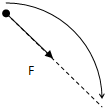
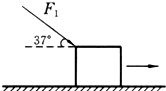 一个质量m=2kg的物体,受到与水平方向成37°角斜向下方的推力F1=10N的作用,在水平地面上移动的距离s=2m,如图所示.物体与地面间的滑动摩擦力为它们间弹力的0.2,取g=10m/s2
一个质量m=2kg的物体,受到与水平方向成37°角斜向下方的推力F1=10N的作用,在水平地面上移动的距离s=2m,如图所示.物体与地面间的滑动摩擦力为它们间弹力的0.2,取g=10m/s2