题目内容
1.绕地球做圆周运动的两颗人造卫星a、b,其轨道半径之比为3:2,则( )| A. | a、b绕地球运行的周期之比为27:8 | |
| B. | a、b绕地球运行的角速度之比为8:27 | |
| C. | a、b绕地球运行的线速度之比为$\sqrt{6}$:3 | |
| D. | a、b绕地球运行的向心加速度之比为3:2 |
分析 卫星运动由万有引力提供向心力即:$\frac{GMm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m{ω}^{2}r=m\frac{4{π}^{2}r}{{T}^{2}}$=ma,列式求出线速度、周期、角速度、向心加速度之比即可.
解答 解:由卫星运动由万有引力提供向心力,根据$\frac{GMm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m{ω}^{2}r=m\frac{4{π}^{2}r}{{T}^{2}}$得:
A、T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,轨道半径之比为3:2,则周期之比为$\sqrt{\frac{27}{8}}$,故A错误;
B、$ω=\sqrt{\frac{GM}{{r}^{3}}}$,轨道半径之比为3:2,则角速度之比为$\sqrt{\frac{8}{27}}$,故B错误;
C、$v=\sqrt{\frac{GM}{r}}$,轨道半径之比为3:2,则线速度之比为$\sqrt{6}$:3,故C正确;
D、a=$\frac{GM}{{r}^{2}}$,轨道半径之比为3:2,则向心加速度之比为4:9,故D错误;
故选:C
点评 本题关键要在理解的基础上能熟练运用万有引力提供向心力计算出卫星的各个量与半径的关系式,难度不大,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
11.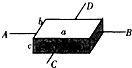 如图所示,是一块均匀的长方体金属块,其长为a,宽为b,高为c,如果沿AB方向测得的电阻为R,那么,该金属块沿CD方向的电阻率和电阻分别为( )
如图所示,是一块均匀的长方体金属块,其长为a,宽为b,高为c,如果沿AB方向测得的电阻为R,那么,该金属块沿CD方向的电阻率和电阻分别为( )
 如图所示,是一块均匀的长方体金属块,其长为a,宽为b,高为c,如果沿AB方向测得的电阻为R,那么,该金属块沿CD方向的电阻率和电阻分别为( )
如图所示,是一块均匀的长方体金属块,其长为a,宽为b,高为c,如果沿AB方向测得的电阻为R,那么,该金属块沿CD方向的电阻率和电阻分别为( )| A. | $\frac{bc}{a}$R,$\frac{{b}^{2}}{{a}^{2}}$R | B. | $\frac{ab}{c}$R,$\frac{{b}^{2}}{{a}^{2}}$R | C. | $\frac{bc}{a}$R,$\frac{b}{a}$R | D. | $\frac{ac}{b}$R,$\frac{{b}^{2}}{{a}^{2}}$R |
9.一列简谐横波沿x轴正方向传播,图甲是波传播到x=5m处M点时的波形图,图乙是x=3m处的质点N从此时刻开始计时的振动图象,Q是位于x=10m处的质点.下列说法正确的是( )


| A. | 这列波的传播速度是1.25m/s | |
| B. | M点以后的各质点开始振动时的方向都沿y轴的负方向 | |
| C. | 质点Q经过5s时,第一次到达波谷 | |
| D. | 在0~8s内,质点P随波沿x轴正方向运动0.8m的距离 |
16.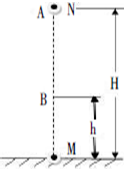 在水平地面上固定一带正电小球M,另有一带电量为q(q>0)、质量为m的小球N,从M球正上方H高处的A点以初速度v0竖直向下运动,当其运动至离地面高h处的B点时返回.若小球N始终在竖直方向运动,运动过程中不计空气阻力,两小球带电量保持不变且可视为质点,重力加速度为g,则下列说法正确的是( )
在水平地面上固定一带正电小球M,另有一带电量为q(q>0)、质量为m的小球N,从M球正上方H高处的A点以初速度v0竖直向下运动,当其运动至离地面高h处的B点时返回.若小球N始终在竖直方向运动,运动过程中不计空气阻力,两小球带电量保持不变且可视为质点,重力加速度为g,则下列说法正确的是( )
 在水平地面上固定一带正电小球M,另有一带电量为q(q>0)、质量为m的小球N,从M球正上方H高处的A点以初速度v0竖直向下运动,当其运动至离地面高h处的B点时返回.若小球N始终在竖直方向运动,运动过程中不计空气阻力,两小球带电量保持不变且可视为质点,重力加速度为g,则下列说法正确的是( )
在水平地面上固定一带正电小球M,另有一带电量为q(q>0)、质量为m的小球N,从M球正上方H高处的A点以初速度v0竖直向下运动,当其运动至离地面高h处的B点时返回.若小球N始终在竖直方向运动,运动过程中不计空气阻力,两小球带电量保持不变且可视为质点,重力加速度为g,则下列说法正确的是( )| A. | 小球N向下运动的过程中,可能一直减速,且加速度大小一直在增大 | |
| B. | 小球N向下运动的过程中,电场力做负功,系统的机械能一直增加 | |
| C. | 小球N向上运动的过程中,最高只能到达A点上方$\frac{{{v}_{0}}^{2}}{2g}$处 | |
| D. | AB两点电势差为UAB=$\frac{2mg(H-h)+m{{v}_{0}}^{2}}{2q}$ |
10.某研究性学习小组用如图1所示装置来测定当地重力加速度,主要操作如下:

①由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t;
②用刻度尺测量出两个光电门之间的高度h,并计算出小铁球通过两光电门间的平均速度$\overline{v}$;
③保持光电门1的位置不变,改变光电门2的位置,重复①的操作.测出多组(h,t),计算出对应的平均速度$\overline{v}$;
④在如图2中画出$\overline{v}$-t图象.
请根据实验,回答如下问题:
(1)设小铁球到达光电门1时的速度为v0,当地的重力加速度为g.则小铁球通过两光电门间平均速度$\overline{v}$的表达式为$\overline{v}$=v0+$\frac{1}{2}$gt;(用v0、g和t表示)
(2)实验测得的数据如表:请在坐标纸上画出$\overline{v}$-t图象;
(3)根据$\overline{v}$-t图象,可以求得当地重力加速度g=9.7m/s2,试管夹到光电门1的距离约为6.2cm.

①由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t;
②用刻度尺测量出两个光电门之间的高度h,并计算出小铁球通过两光电门间的平均速度$\overline{v}$;
③保持光电门1的位置不变,改变光电门2的位置,重复①的操作.测出多组(h,t),计算出对应的平均速度$\overline{v}$;
④在如图2中画出$\overline{v}$-t图象.
请根据实验,回答如下问题:
(1)设小铁球到达光电门1时的速度为v0,当地的重力加速度为g.则小铁球通过两光电门间平均速度$\overline{v}$的表达式为$\overline{v}$=v0+$\frac{1}{2}$gt;(用v0、g和t表示)
(2)实验测得的数据如表:请在坐标纸上画出$\overline{v}$-t图象;
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| h(cm) | 10.00 | 20.00 | 30.00 | 40.00 | 50.00 | 60.00 |
| t(s) | 0.069 | 0.119 | 0.159 | 0.195 | 0.226 | 0.255 |
| $\overline{v}$(m/s) | 1.45 | 1.68 | 1.89 | 2.05 | 2.21 | 2.35 |
11. 如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
 如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )| A. | 物体甲所受的摩擦力可能为零 | B. | 物体甲一定受到四个力作用 | ||
| C. | 物体乙所受的摩擦力可能为零 | D. | 水平面对斜面体无摩擦力作用 |

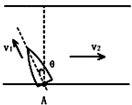 如图所示,某小船从河岸的A点出发,保持船身与垂直河岸的方向成θ=37°的方向朝河对岸匀速行驶,小船在静水中的速度为v1=6m/s,河水的速度为v2=10m/s且保持不变,河宽为96m,则小船过河的时间为20s.
如图所示,某小船从河岸的A点出发,保持船身与垂直河岸的方向成θ=37°的方向朝河对岸匀速行驶,小船在静水中的速度为v1=6m/s,河水的速度为v2=10m/s且保持不变,河宽为96m,则小船过河的时间为20s.