题目内容
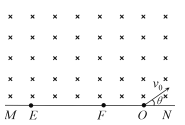
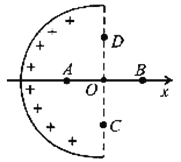
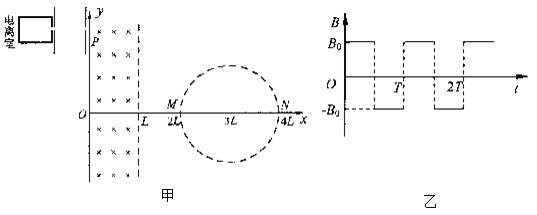
【题目】如图甲所示，在直角坐标系中的0≤x≤L区域内有垂直纸面向里的匀强磁场，以点(3L，0)为圆心、半径为L的圆形区域，与x轴的交点分别为M、N．在xOy平面内，从电离室产生的质量为m，带电量为e的电子以几乎为零的初速度飘入电势差为U的加速电场中，加速后经过右侧极板上的小孔沿x轴正向由y轴上的P点进入到磁场，飞出磁场后从M点进入圆形区域时，速度方向与x轴夹角为60o，此时在圆形区域加如图乙所示的周期性变化的磁场，以垂直于纸面向外为磁场正方向，电子运动一段时间后从N点飞出，速度方向与M点进入磁场时的速度方向相同．求：
(1)P的纵坐标；
(2) 0≤x≤L区域内匀强磁场磁感应强度B的大小；
(3)写出圆形磁场区域磁感应强度B0的大小、磁场变化周期T各应满足的表达式．
【答案】（1）
（2）
（3）
【解析】（1）电子在矩形磁场区域做圆周运动，出磁场后做直线运动，其轨迹如图所示
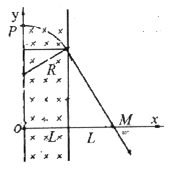
由几何关系有：
，
（2）由动能定理
，可得
，又
把几何关系代入解得
（3）在磁场变化的半个周期内粒子的偏转角为120°，根据几何知识，在磁场变化的半个周期内，粒子在x轴方向上的位移恰好等于
，粒子到达N点而且速度符合要求的空间条件是：
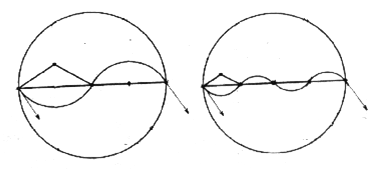
电子在磁场做圆周运动的轨道半径
解得
（n=1.2.3…..）
粒子在磁场变化的半个周期恰好转过
圆周，同时MN间运动时间是磁场变化周期的整数倍，可使粒子到达N点并且速度满足题设要求，应满足的时间条件：
又
，解得
（n=1.2.3.4…….）
练习册系列答案
相关题目
