题目内容
2.光滑水平面上两个质量相等的小球A、B相距L,两球初速度均为零,A球在水平向右的恒力作用下以加速度a正对B球方向做匀加速直线运动,已知两球正面碰撞后彼此交换速度,A碰撞前后加速度不变,B撞断撞前后加速度均为零,第5次碰撞点与A的出发点间距为41L,第79次碰撞后B的速度大小为$79\sqrt{2aL}$.分析 第一次碰撞时A速度由${v}_{1}^{2}=2aL$求得,碰后A的速度为0,B做速度为v1的匀速运动,当第二次碰前A速度为2v1,则碰后B的速度为2v1,A的速度为v1;第三次碰前A的速度为3v1.则碰后B的速度为3v1,A的速度为2v1,第四次碰前A的速度为4v1,碰后B的速度为4v1,A的速度为3v1,可推出第n次碰后,B的速度为nv1,A的速度为(n-1)v1
解答 解:第一次碰撞时A速度由:${v}_{1}^{2}=2aL$
得${v}_{1}=\sqrt{2aL}$
则碰后B的速度为:
${v}_{1}=\sqrt{2aL}$
碰后A的速度为0;
第二次碰撞满足:$\frac{1}{2}a{t}^{2}={v}_{1}t$
解得t=$\frac{2{v}_{1}}{a}$
所以第二次碰撞前A的速度为$at=a\frac{2{v}_{1}}{a}=2{v}_{1}$
由此可以推断第n次碰撞前A的速度为nv1
所以第5次碰撞点据A出发点的距离x=xB+L
又${x}_{B}=({v}_{1}+2{v}_{1}+3{v}_{1}+4{v}_{1})×\frac{2{v}_{1}}{a}$
所以$x=\frac{20{v}_{1}^{2}}{a}$+L=41L
第79次碰撞后B的速度即为碰撞前A的速度,据第n次碰撞前A的速度为nv1,可得此时B的速度
${v}_{B}=79{v}_{1}=79\sqrt{2aL}$
故答案为:41L,$79\sqrt{2aL}$.
点评 考查速度位移公式,明确v2=2aL.注意逻辑推理后面的碰撞,要细心找出碰撞规律是解决问题的关键.

练习册系列答案
相关题目
13.一个从静止开始做匀加速直线运动的物体,从开始运动起连续通过三段位移的时间分别是1s、2s、3s,下列选项中正确的是( )
| A. | 这三段位移的长度之比1:22:32 | |
| B. | B.这三段位移的长度之比1:23:33 | |
| C. | 这三段位移上的平均速度之比1:2:3 | |
| D. | 这三段位移上的平均速度之比1:22:32 |
10.下列说法不正确的是( )
| A. | 对人体的安全电压是不高于36 V | |
| B. | 家庭电路中的插座应与灯座并联起来 | |
| C. | 在家庭电路中可以用钢丝代替保险丝 | |
| D. | 电能表是用来测量用户消耗电能的仪表 |
11.第一次用水平恒力F作用在物体上,使物体在光滑水平面上移动距离l,F做功W1,第二次用同样大的力F沿斜面方向作用于物体上,使物体沿粗糙斜面移动的距离也是l,F做功W2,那么( )
| A. | W1>W2 | B. | W1=W2 | C. | W1<W2 | D. | 无法判断 |
12. 如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
 如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )| A. | 当增大两板间距离时,v增大 | |
| B. | 当减小两板间距离时,v增大 | |
| C. | 当增大两板间距离时,电容器的电量增大 | |
| D. | 当减小两板间距离时,电容器的电量增大 |
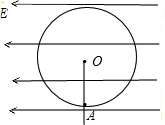 如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏高竖直方向的最大角度θ=74°.
如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏高竖直方向的最大角度θ=74°.