题目内容
19.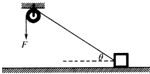 如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )
如图所示,用一恒力F通过一定滑轮拉动一箱子,箱子的质量为m,箱子与地面的动摩擦因数为μ,某时刻绳与水平面的夹角为θ,绳端的速度为v,不计绳与滑轮的摩擦,重力加速度为g,则该时刻( )| A. | 箱子的速度大小为vcosθ | B. | 箱子的加速度方向一定向左 | ||
| C. | 箱子的加速度大小为$\frac{Fcosθ}{m}$-μg | D. | 恒力做功功率为Fv |
分析 将箱子的速度方向分解为沿绳子方向和垂直绳子方向,结合平行四边形定则求出箱子的速度表达式,得出箱子的运动规律,从而确定加速度的方向.根据牛顿第二定律求出箱子的加速度.根据功率的公式求出恒力F的瞬时功率.
解答 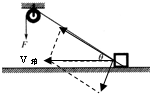 解:A、根据平行四边形定则知,箱子的速度${v}_{箱}=\frac{v}{cosθ}$,箱子向左运动的过程中,θ变大,则箱子的速度变大,则加速度方向向左,故A错误,B正确.
解:A、根据平行四边形定则知,箱子的速度${v}_{箱}=\frac{v}{cosθ}$,箱子向左运动的过程中,θ变大,则箱子的速度变大,则加速度方向向左,故A错误,B正确.
C、根据牛顿第二定律得,箱子的加速度大小a=$\frac{Fcosθ-μ(mg-Fsinθ)}{m}$,故C错误.
D、恒力做功的功率P=Fv,故D正确.
故选:BD.
点评 本题关键是找出合运动与分运动,然后由平行四边形定则找出合速度与分速度间的几何关系,或列出解析式讨论;切记不可将绳子速度当成合速度.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.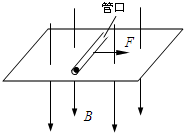 如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )
如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )
 如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )
如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )| A. | 小球带正电 | |
| B. | 离开试管前洛伦兹力对小球做正功,离开试管后洛伦兹力对小球不做功 | |
| C. | 离开试管前小球运动的轨迹是一条抛物线 | |
| D. | 离开试管后沿着磁感线方向可以看到小球做逆时针方向的圆周运动 |
4.关于电场下列说法正确的是( )
| A. | 在点电荷产生的电场中,以点电荷为中心的同一圆周上,场强处处相同 | |
| B. | 在表达式E=$\frac{kQ}{{r}^{2}}$中,Q为场源电荷电量 | |
| C. | 若将点电荷在电场中由静止释放,则电荷的运动轨迹一定与电场线重合 | |
| D. | 沿着电场线方向,场强一定减小 |
9. 两个较大的平行板A、B相距为d,分别接在电压为U的电源正负极上,开关S闭合时质量为m,带电量为-q的油滴恰好静止在两板之间,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
两个较大的平行板A、B相距为d,分别接在电压为U的电源正负极上,开关S闭合时质量为m,带电量为-q的油滴恰好静止在两板之间,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
 两个较大的平行板A、B相距为d,分别接在电压为U的电源正负极上,开关S闭合时质量为m,带电量为-q的油滴恰好静止在两板之间,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )
两个较大的平行板A、B相距为d,分别接在电压为U的电源正负极上,开关S闭合时质量为m,带电量为-q的油滴恰好静止在两板之间,如图所示.在保持其他条件不变的情况下,将两板缓慢地水平错开一些,以下说法正确的是( )| A. | 两板间电压不变,电容变小 | B. | 油滴将静止不动 | ||
| C. | 电流计中的电流从a流向b | D. | 电流计中的电流从b流向a |

 相距为L的点电荷A、B带电荷量分别为+9Q和-Q,如图所示,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则第三个电荷C应带何种电荷、应放置何处、电荷量是多少?
相距为L的点电荷A、B带电荷量分别为+9Q和-Q,如图所示,今引入第三个点电荷C,使三个点电荷都处于平衡状态,则第三个电荷C应带何种电荷、应放置何处、电荷量是多少? 如图所示的电路中,AB两端的电压U恒为14V,灯泡L标有“6V、12W”字样,电动机线圈的电阻RM=0.5Ω.若灯泡恰能正常发光,且电机能运转,求
如图所示的电路中,AB两端的电压U恒为14V,灯泡L标有“6V、12W”字样,电动机线圈的电阻RM=0.5Ω.若灯泡恰能正常发光,且电机能运转,求