��Ŀ����
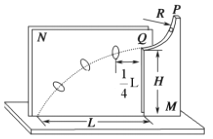
����Ŀ��ͬѧ�Dz���٤����ʱ����ʾƽ���˶��ķ�����������ͼ��ʾ��ʵ��װ�á�ͼ��ˮƽ���õĵװ�����ֱ�ع̶���M���N�壬M���ϲ���һ�뾶ΪR��һԲ���εĴֲڹ����PΪ��ߵ㣬aΪ��͵㣬Q�㴦������ˮƽ����װ��ΪH��N���Ϲ̶�������Բ����������Ϊm��С���P����ֹ�ͷţ�С���˶���Q�ɳ������谭��ͨ���������ģ��䵽�װ��Ͼ�Q ˮƽ����ΪL ���������ǿ����������������ٶ�Ϊg����(1)С���˶���Q��ʱ�ٶȵĴ�С�Լ��Թ��ѹ����
(2)��Qˮƽ����Ϊ![]() L��Բ�����ĵ��װ�ĸ߶ȡ�
L��Բ�����ĵ��װ�ĸ߶ȡ�
���𰸡�(1) 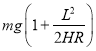 ��������ֱ����(2)
��������ֱ����(2) ![]()
�������������������1������ƽ���˶����ص㣬�������С���˶���Q��ʱ�ٶȵĴ�С����Q��С���ܵ���֧�����������ĺ����ṩ����������ţ�ٵڶ����ɼ������С���ܵ���֧�����Ĵ�С����ţ�ٵ�������˵���Թ��ѹ���Ĵ�С�ͷ���2������ƽ���˶����ص㣬���˶��ֽ⼴�����.
��1����ƽ���˶��Ĺ��ɣ����У� ![]() ��
�� ![]()
��ã� ![]()
��ţ�ٵڶ����ɣ��ɵ���Q���У� ![]()
��ã� ![]()
����ţ�ٵ������ɣ���С����Q��Թ����ѹ���� ![]() ��������ֱ����
��������ֱ����
��2�������˶�ѧ��ʽ���У� ![]() ��
�� ![]()
��ã� ![]()
���Ծ�Qˮƽ����Ϊ![]() ��Բ��������װ�ĸ߶�
��Բ��������װ�ĸ߶�![]()

 ��У����ϵ�д�
��У����ϵ�д�