��Ŀ����
����Ŀ����ͼ����ʾ���ù̶��ĵ綯��ˮƽ��������m=2kg��С��������M=1kg��ƽ������ͬ���ٶ�һ�����������˶������λ��ƽ����࣬����Ϊ�ʵ㣮��ƽ����Ҳ�һ�����봦��̨���赲��ƽ��ײ�Ϻ������ֹͣ�˶����綯�����ʱ���P=3W���䣮��ijʱ��t=0�𣬲�������ٶ���ʱ��ı仯��ϵ��ͼ����ʾ��t=6s�����Ϊ�����˶���t=10sʱ����뿪ľ�壮�������ٶ�g=10m/s2 �� ��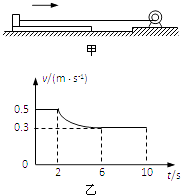
��1��ƽ��������Ķ�Ħ��������Ϊ���
��2�������1sĩ��3sĩ�ܵ���Ħ������Ϊ���
��3��ƽ�峤��LΪ���٣�
���𰸡�
��1��
�⣺��0��2s��������һ����0.5m/s���ٶ������˶������У�
P=F1v1
���������������˶�������������Ħ��������F1=f
�������Ħ����Ϊ��f=��N=�̣�M+m��g
�������ݵã���=0.2
��2��
�⣺1sʱ�̣�������٣����ӵ���������ƽ������ľ�Ħ�������ָ���ƽ�������˶���֪����ƽ��ľ�Ħ�������ڶ����ƽ��Ļ���Ħ������
f1=�̣�M+m��g=6N
��ͼ��֪��2sʱ��ʼƽ��ײ��̨���Ͼ�ֹ������鿪ʼ��ƽ�����ȼ����˶����ʻ������ܵ�Ħ����Ϊ����Ħ���������ھ�ֹǰĦ�����Ĵ�С���ֲ��䣮
��3sʱ�̣������ľ���ϻ��������Ի������ܵ�Ħ����Ϊ����Ħ������
��Ϊ��������ٴ�����ʱ�ٶ�Ϊ��
v2=0.3m/s
P=F2v2
��F1V1=F2V2
F2=f2=10N
��3��
�⣺�����ƽ���ϼ����˶���ʱ��Ϊ��t=6��2=4s��
�����������е�������Ĺ�W=Pt��Ħ����ʼ��Ϊ����Ħ��������СΪ��f2=10N��
�ɶ��ܶ����У�
Pt��f2L1= ![]() mv22��
mv22�� ![]() mv12
mv12
��L1=1.184m
������ƽ���������˶���ʱ���ǣ�t��=10��6=4s
�����˶���λ�ƣ�L2=v2t��=0.3��4=1.2m
ƽ����ܳ��ȣ�L=L1+L2=1.184m+1.2m=2.384m
����������1����Ȼ��0��2s�����������˶����������ڵ����ƽ���Ħ����������P=FV����������ܵ�Ħ������Ȼ�����f=��FN�����Ħ�������̣���2����t=2s��ƽ�岻����������ܵ�Ħ����Ϊƽ������Ļ���Ħ������ֱ����������˶�Ħ���������ֲ��䣬��P=FV��֪���������˶�ʱ��Ħ�����Ӷ����������3sĩ���ܵĻ���Ħ����f2 �� ��3������ͼ���֪������t=2s��ʼ��ƽ���ϻ�������6sʱ�뿪ƽ�壬����ƽ���ϻ���4s������ͼ���֪�����ƽ���ϻ���ʱ���ٶ�Ϊ0.3m/s�����������Ĺ�ΪPt������Եص�λ�Ƽ�ƽ��ij��ȣ��Ӷ�����֪��Ħ���������Ĺ��±���ʽf2L���������ö��ܶ����������ƽ��ij���L��
�����㾫����������Ҫ������V-tͼ��Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ����v-tͼ�����ٶ�ͼ���У����Զ����������κ�ʱ�̵��ٶȣ������ٶ�ͼ���У�������һ��ʱ���ڵ�λ�ƴ�С����������ٶ�ͼ�������ʱ������Χ�����ֵ�������ٶ�ͼ���У�����������ʱ�̵ļ��ٶȾ����ٶ�ͼ��������Ӧ�ĵ�����ߵ�б�ʣ���ͼ������ύ�棬��ʾ�����˶����ٶȷ���ͼ����ֱ�߱�ʾ�������ȱ���ֱ���˶�������ֱ���˶�;ͼ�������߱�ʾ������������˶���Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�