题目内容
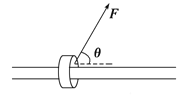
【题目】将质量m=0.1kg的圆环套在固定的水平直杆上，环的直径略大于杆的截面直径，环与杆的动摩擦因数μ=0.8。刚开始环处于静止，现对环施加一位于竖直平面内斜向上与杆夹角θ=53°的恒定拉力F，使圆环从静止开始沿杆向右匀加速，经过t=
s后撤去拉力F发现继续前进1m后静止（取g=10m/s2，（sin53°=0.8，cos53°=0.6）。求：
（1）撤去拉力F瞬间圆环的速度大小；
（2）圆环加速时的加速度大小；
（3）拉力F的大小。
【答案】（1）4m/s （2）4.4m/s2 （3）1N或9N
【解析】
(1) 撤去拉力F后，圆环受到重力，支持力，和摩擦力，由牛顿第二定律可知：
，
所以：
；
由
得：
；
（2）小环做匀加速直线运动，由运动学公式可知：
；
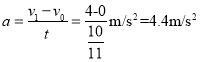(3)当环不受弹力时，
，
代入数据解得：
当F<1.25N时，环与杆上部接触,受杆向上的支持力FN，
由牛顿第二定律可知
，
，
又：
解得：
；
当F>1.25N时，环与杆下部接触，受杆向下的压力
由牛顿第二定律可知：
，
，
又：
，
解得：
；
【题目】某同学用图（a）所示的装置测量木块与木板之间的动摩擦因数。跨过光滑定滑轮的细线两端分别与木块和弹簧测力计相连，滑轮和木块间的细线保持水平，在木块上方放置砝码缓慢向左拉动水平放置的木板，当木块和砝码相对桌面静止且木板仍在继续滑动时，弹簧测力计的示数即为木块受到的滑动摩擦力的大小。某次实验所得数据已在下表中给出，其中
的值可从图（b）中弹簧测力计的示数读出。
砝码的质量 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 |
滑动摩擦力 | 2.15 | 2.36 | 2.55 |
| 2.93 |
回答下列问题：
（1）=__________
：
（2）在图（c）的坐标纸上补齐未画出的数据点并绘出
图线____________；
（3）
与
、木块质量
、木板与木块之间的动摩擦因数
及重力加速度大小
之间的关系式为=__________，图线（直线）的斜率的表达式为
=__________。
（4）取
，由绘出的
图线求得
_____。（保留2位有效数字）
