题目内容
【题目】小明设计了一个弹球游戏装置，如图所示，ABCD为四分之三圆弧轨道，A端通过竖直过渡轨道PA与弹射装置相连，D端通过水平过渡轨道DE与水平轨道EG相连，两过渡轨道稍微错开；管径很小的圆形细管
与轨道EG相切于O点，细管底部进出口O、
稍微错开，整个轨道固定于同一竖直平面内，各段轨道间均平滑连接。现有一小球（可视为质点）被压缩的轻弹簧从P点弹出后沿轨道运动。已知小球质量m=0.2kg，轨道ABCD的半径r=0.1m，细管的圆半径R=0.2m，P、A两点间的高度差h=0.5m，O、E两点间的距离L=1m，O、G两点间的距离足够大，小球与轨道EG间的动摩擦因数
，其余轨道均光滑，弹簧的最大弹性势能Epm=2.2J弹簧的形变始终不超过其弹性限度，小球运动时始终未脱离轨道。
(1)求小球通过B点的最小速度和对应的弹簧弹性势能；
(2)为使小球最终停在EO段，求弹簧弹性势能应满足的条件；
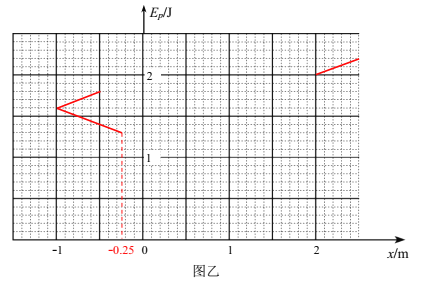
(3)以O点为坐标原点，O点指向G点的方向为正方向建立x轴，在图乙中画出弹簧弹性势能Ep与小球最终停下的位置坐标x的关系图线（本小题不需要写出具体解答过程，但需要标出关键点的坐标值）。
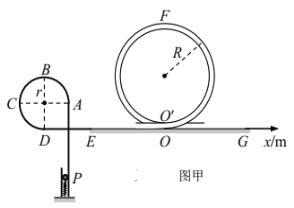
【答案】(1)1m/s，1.3J；(2)1.3J≤Ep≤1.8J；(3)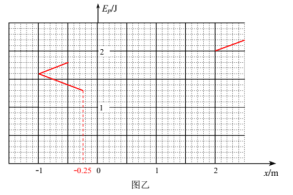
【解析】
（1）在B点，当轨道对小球的弹力恰好为零时，根据向心力公式有
解得
vB=1m/s
从P点到B点，根据功能关系有
Ep1=mg（h+r）+
解得
Ep1=1.3J
（2）若小球恰好到达F点，从P点到F点，根据功能关系有
Ep2=mg（h-r+2R）+μmgL
解得
Ep2=2J
此后小球返回，根据功能关系有
mg·2R=mgh1+μmgL
解得
h1=0.2m=2r＞r=0.1m
小球会在CB间脱离轨道
若小球在到达F点前返回恰好到达C点，从P点到C点，根据功能关系有:
Ep3=mgh+μmg·2L
解得
Ep3=1.8J
故要使小球最终停在EO段，弹簧弹性势能应满足
1.3J≤Ep3≤1.8J
（3）当Ep>2J时，小球停在OG段，根据功能关系有
Ep=-mg（h-r）+μmg（L+x）
解得
Ep=0.4x+1.2 （2m＜x≤2.5m）
当1.3J≤Ep3≤1.8J时，小球停在EO段；当小球在EO段恰好往返一次到E点时，根据功能关系有
Ep4=mg·（h-r）+μmg·2L
解得
Ep4=1.6J
当
1.3J≤Ep3<1.6J
时，根据功能关系有
Ep=mg（h-r）+μmg（L+x）
解得
Ep=-0.4x+1.2 （-1m＜x≤-0.25m）
当1.6J≤Ep3≤1.8J时，根据功能关系有
Ep=-mg·（h-r）+μmg{（2L+[L-（-x）]}
解得
Ep=0.4x+2 （-1m≤x≤-0.5m）
图线如图所示:
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
