题目内容
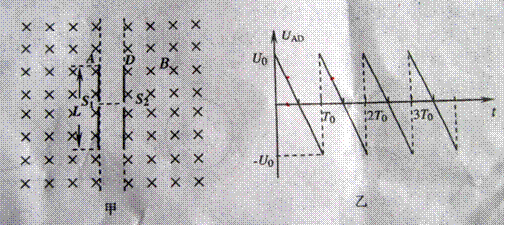
如图甲,距离很近的竖直边界两侧为相同的匀强磁场区域,磁场范围很大,方向垂直纸面向里.在边界上固定两个等长的平行金属板A 和D,两金属板中心各有-小孔S1、S2,板间电压的变化规律如图乙,正、反向最大电压均为U0,周期为T0.一个质量为m、电荷量为+q 的粒子在磁场中运动的周期也是T0.现将该粒子在t=T0/4时刻由S1 静止释放,经电场加速后通过S2又垂直于边界进人右侧磁场区域,在以后的运动过程中不与金属板相碰.不计粒子重力、极板外的电场及粒子在两边界间运动的时间.
( l )求金属板的最大长度.
( 2 )求粒子第n 次通过S2的速度.
( 3)若质量m′=13/12m 电荷量为+q 的另一个粒子在t=0 时刻由S1静止释放,求该粒子在磁场中运动的最大半径.

( l )求金属板的最大长度.
( 2 )求粒子第n 次通过S2的速度.
( 3)若质量m′=13/12m 电荷量为+q 的另一个粒子在t=0 时刻由S1静止释放,求该粒子在磁场中运动的最大半径.

分析:(1)粒子在匀强电场中做匀加速直线运动,电场力做功等于粒子动能的增加;使粒子不与极板相撞,则运动的半径大于
;
(2)粒子在磁场中D的运动轨迹是两个半圆,所以在磁场中运动的时间就是一个周期,也是T0.每次加速的电压总为
;
(3)质量m′=13/12m 电荷量为+q 的另一个粒子在t=0 时刻由S1静止释放,它在磁场中的周期:T=
=
?
=
T0,所以粒子第二次被加速时的电压是
U0,第三次被加速时的电压是
U0,…分析可知,粒子被连续加速6次后,圆周运动的半径最大.
| L |
| 2 |
(2)粒子在磁场中D的运动轨迹是两个半圆,所以在磁场中运动的时间就是一个周期,也是T0.每次加速的电压总为
| U0 |
| 2 |
(3)质量m′=13/12m 电荷量为+q 的另一个粒子在t=0 时刻由S1静止释放,它在磁场中的周期:T=
| 2πm′ |
| qB |
| 13 |
| 12 |
| 2πm |
| qB |
| 13 |
| 12 |
| 5 |
| 6 |
| 4 |
| 6 |
解答:解:(1)由题意知,粒子第一次在电场中运动,由动能定理有 q
=
mv02
粒子在磁场里做匀速圆周运动,有qvB=m
周期 T0=
半径 r=
在磁场里做匀速圆周运动的最小半径r=
解得金属板的最大长度 L=
(2)粒子每从S1、S2中穿过一次,就会被加速一次,且每次加速的电压总为
对粒子由动能定理有 n
q=
mvn2
解得vn=
(3)质量m′=13/12m 电荷量为+q 的另一个粒子在磁场中的周期:T=
=
?
=
T0
所以粒子第二次被加速时的电压是
U0,第三次被加速时的电压是
U0,…
分析可知,粒子被连续加速6次后,圆周运动的半径最大,记为r6
第1次加速过程中,由动能定理有 U0q=
m′v12-0
第2次加速过程中,有
U0q=
m′v22-
m′v12
…
第6次加速过程中,有
U0q=
m′v62-
m′v52
以上6式左右累加解得 v6=
由qBv6=m′
得 r6=
答:(l)金属板的最大长度L=
.
(2)粒子第n 次通过S2的速度vn=
.
(3)该粒子在磁场中运动的最大半径r6=
.
| U0 |
| 2 |
| 1 |
| 2 |
粒子在磁场里做匀速圆周运动,有qvB=m
| v2 |
| R |
周期 T0=
| 2πm |
| qB |
半径 r=
| mv0 |
| qB |
在磁场里做匀速圆周运动的最小半径r=
| L |
| 4 |
解得金属板的最大长度 L=
| 2T0 |
| π |
|
(2)粒子每从S1、S2中穿过一次,就会被加速一次,且每次加速的电压总为
| U0 |
| 2 |
对粒子由动能定理有 n
| U0 |
| 2 |
| 1 |
| 2 |
解得vn=
|
(3)质量m′=13/12m 电荷量为+q 的另一个粒子在磁场中的周期:T=
| 2πm′ |
| qB |
| 13 |
| 12 |
| 2πm |
| qB |
| 13 |
| 12 |
所以粒子第二次被加速时的电压是
| 5 |
| 6 |
| 4 |
| 6 |
分析可知,粒子被连续加速6次后,圆周运动的半径最大,记为r6
第1次加速过程中,由动能定理有 U0q=
| 1 |
| 2 |
第2次加速过程中,有
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
…
第6次加速过程中,有
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
以上6式左右累加解得 v6=
|
由qBv6=m′
| v62 |
| r6 |
| T0 |
| π |
|
答:(l)金属板的最大长度L=
| 2T0 |
| π |
|
(2)粒子第n 次通过S2的速度vn=
|
(3)该粒子在磁场中运动的最大半径r6=
| T0 |
| π |
|
点评:该题类似于回旋加速器,第三问中分析出粒子被连续加速6次后,圆周运动的半径最大.是解题的关键.该题解题的过程复杂,公式较多,容易在解题的过程中出现错误.属于难度大的题目.

练习册系列答案
相关题目